Calculate Brick Velocity & Draw Displacement-Time Graph

[mathlearn]

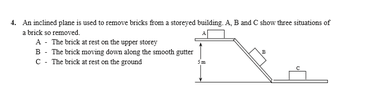
View attachment 6143

Calculate the velocity of the brick at the bottom of the inclined plane.

State the assumption you made for your calculation in part above.

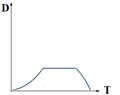
& Sketch the displacement-time graph relevant to the movement of the brick along the smooth gutter. (Assume that the brick started to move from the state of rest.)

Workings:

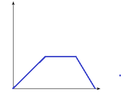
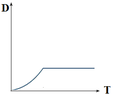
I am unable to think on the first two but I think the displacement and time graph should be something like ,

View attachment 6144

Many Thanks :)

 

[MarkFL]

To calculate the velocity of the brick at the bottom of the gutter, I would take the statement that the gutter is smooth to mean there is no friction, and so conservation of energy can be applied. When the brick is at the top of the gutter, it has gravitational potential energy, and since it begins from rest it has no kinetic energy. Then when the brick is at the bottom of the gutter it has kinetic energy, but no gravitational energy. The amount of energy stays the same, but it changes from potential energy to kinetic energy.

So, if we equate the initial potential energy to the final kinetic energy, we have:

$$mgh=\frac{1}{2}mv^2$$

What do you get upon solving for $v$?

 

[mathlearn]

To calculate the velocity of the brick at the bottom of the gutter, I would take the statement that the gutter is smooth to mean there is no friction, and so conservation of energy can be applied. When the brick is at the top of the gutter, it has gravitational potential energy, and since it begins from rest it has no kinetic energy. Then when the brick is at the bottom of the gutter it has kinetic energy, but no gravitational energy. The amount of energy stays the same, but it changes from potential energy to kinetic energy.

So, if we equate the initial potential energy to the final kinetic energy, we have:

$$mgh=\frac{1}{2}mv^2$$

What do you get upon solving for $v$?

Thank you very much MarkFL (Party)(Smile)

$$mgh=\frac{1}{2}mv^2$$

$$2kg * 10 ms^-2 * 5 m=\frac{1}{2}mv^2$$

$$2kg * 10 ms^-2 * 5 m=\frac{1}{2}*2kg * v^2$$

$$2kg * 10 ms^-2 * 5 m=\frac{1}{2}*2kg * v^2$$

$$100 J= v^2$$

$$10 J= v$$

Correct ? :)

 

[MarkFL]

I would solve the equation first, and then plug in the numbers:

$$mgh=\frac{1}{2}mv^2$$

$$v=\sqrt{2gh}$$

Okay, at this point we can plug in:

$$g\approx9.81\,\frac{\text{m}}{\text{s}^2},\,h=5\text{ m}$$

$$v\approx\sqrt{2\left(9.81\,\frac{\text{m}}{\text{s}^2}\right)\left(5\text{ m}\right)}=3\sqrt{\frac{109}{10}}\,\frac{\text{m}}{\text{s}}\approx9.9045\,\frac{\text{m}}{\text{s}}$$

 

[mathlearn]

I would solve the equation first, and then plug in the numbers:

$$mgh=\frac{1}{2}mv^2$$

$$v=\sqrt{2gh}$$

Okay, at this point we can plug in:

$$g\approx9.81\,\frac{\text{m}}{\text{s}^2},\,h=5\text{ m}$$

$$v\approx\sqrt{2\left(9.81\,\frac{\text{m}}{\text{s}^2}\right)\left(5\text{ m}\right)}=3\sqrt{\frac{109}{10}}\,\frac{\text{m}}{\text{s}}\approx9.9045\,\frac{\text{m}}{\text{s}}$$

Thank you very much :D

:D speaking about the graph

Sketch the displacement-time graph relevant to the movement of the brick along the smooth gutter. (Assume that the brick started to move from the state of rest.)

View attachment 6145

Is the above drawn graph correct?

 

[MarkFL]

For the graph, you have the brick returning to its original position, since the ending value is zero. Also, the acceleration will be constant as it moves down the gutter, so what kind of curve should we use?

 

[I like Serena]

speaking about the graph

Is the above drawn graph correct?

Hey mathlearn! ;)

Here's what the acceleration and speed graphs would look like (using our new TikZ drawing capabilities ):
\begin{tikzpicture}[ultra thick]
\draw[red] (0,5) node[above] {\Large $a$} -- (5,5) -- (5,0) -- (10,0);
\draw[blue] (0,0) node[above] {\Large $v$} -- (5,3) -- (10,3);
\end{tikzpicture}
On the inclined plane we have a constant acceleration, and when it ends, the acceleration becomes near zero.
As a result the speed increases linearly until the end of the slope, after which the speed remains constant (although in reality it would linearly decrease slowly until zero).
Note that $v=\int_0^t a\,dt$.

However, we're asked for the displacement, which we can call $d$.
We have that $d=\int_0^t v\,dt$.
What would the displacement graph look like? (Wondering)

 

[topsquark]

$$100 J= v^2$$

$$10 J= v$$

Recheck your units, speed is not measured in J. (And the square root of a J is not J!)

-Dan

 

[mathlearn]

For the graph, you have the brick returning to its original position, since the ending value is zero. Also, the acceleration will be constant as it moves down the gutter, so what kind of curve should we use?

View attachment 6147

This kind of a curve :) with constant acceleration and with deceleration.

Hey mathlearn! ;)

Here's what the acceleration and speed graphs would look like (using our new TikZ drawing capabilities ):
\begin{tikzpicture}[ultra thick]
\draw[red] (0,5) node[above] {\Large $a$} -- (5,5) -- (5,0) -- (10,0);
\draw[blue] (0,0) node[above] {\Large $v$} -- (5,3) -- (10,3);
\end{tikzpicture}
On the inclined plane we have a constant acceleration, and when it ends, the acceleration becomes near zero.
As a result the speed increases linearly until the end of the slope, after which the speed remains constant (although in reality it would linearly decrease slowly until zero).
Note that $v=\int_0^t a\,dt$.

However, we're asked for the displacement, which we can call $d$.
We have that $d=\int_0^t v\,dt$.
What would the displacement graph look like? (Wondering)

The displacement time graph would look like the above graph

Recheck your units, speed is not measured in J. (And the square root of a J is not J!)

-Dan

Thanks for the catch :)

 

[MarkFL]

This kind of a curve :) with constant acceleration and with deceleration...

Why do you have the brick returning to zero displacement?

 

[mathlearn]

Why do you have the brick returning to zero displacement?

:) Then is the graph without returning to zero displacement

View attachment 6148

 

[I like Serena]

:) Then is the graph without returning to zero displacement

For the record, you're assuming that the brick ends up in sand at the bottom of the slope, coming to an abrupt stand still.
The corresponding graphs then look like:
\begin{tikzpicture}[font=\LARGE]
\draw[thick, gray, ->] (0,0) -- (9,0) node

{$t$};
\draw[thick, gray, ->] (0,-6) -- (0,4.5);
\draw[ultra thick, red] (0,2) node

{$a$} -- (5,2) -- (5,-6) -- (6,-6) -- (6,0) -- (8,0);
\draw[ultra thick, blue] (0,0) -- (5,4) -- (6,0) -- (8,0) node[above] {$v$};
\draw[ultra thick, olive] (0,0) parabola (5,3) parabola bend (6,3.6) (6,3.6) -- (8,3.6) node

{$d$};
\end{tikzpicture}
(Just had to make the TikZ drawing. )​