- #1
mcas
- 24
- 5
- Homework Statement
- Write a Matlab code that plots the conductivity dependence of temperature for a semiconductor.
- Relevant Equations
- [itex]\sigma = q(n\mu_n + p\mu_p[/itex]
[itex]\frac{1}{\mu} = \frac{1}{\mu_I} + \frac{1}{\mu_L} [/itex]
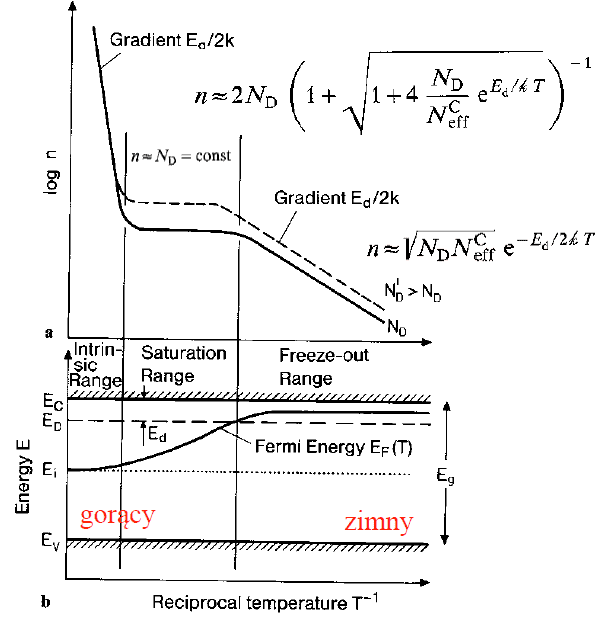
[itex] n \approx 2N_D \left(1 + \sqrt{1 + 4\frac{N_D}{N_C}e^{E_d / kT}}\right)^{-1}[/itex]
I have to plot the conductivity dependence of temperature and I have problems with obtaining the right dependency of [itex]\mu[/itex] and [itex]n[/itex]. But let's focus only on carrier concentration first.
For [itex]n[/itex] I used the third equation. From what I understand [itex]N_D[/itex] is a constant. I want my plot to look like this:
But instead, it looks like this:
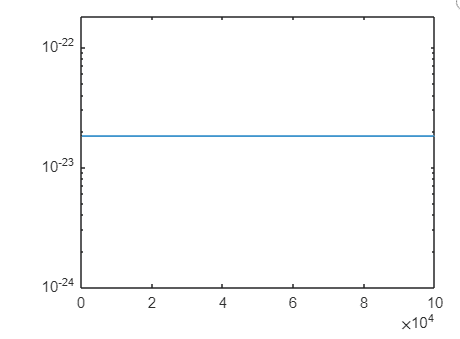
Here is the code:
The calculations are made for silicon. I really don't know why I can't get this right.
For [itex]n[/itex] I used the third equation. From what I understand [itex]N_D[/itex] is a constant. I want my plot to look like this:
But instead, it looks like this:
Here is the code:
carrier concentration calculation:
n_0 = 4.0*10^(15);
N_c = @(x) 6.2 * 10^15 * x^(3/2);
N_v = @(x) 3.5 * 10^15 * x^(3/2);
E_g = @(x) 1.17 - 4.73 *10^(-4) * x^2 / (x + 636);
k = 8.61733262*10^(-5);
n_i = @(x) sqrt(N_c(x) * N_v(x)) * exp(- E_g(x)./ (2 * x.*k));
E_F = @(x) k * x* log(n_i(x).\n_0) + E_g(x)./ 2;
E_d = @(x) E_g(x)- E_F(x);
n_D = 10^20;
n = @(x) 2 * n_D* (1 + sqrt(1 + 4 * n_D ./ N_c(x).* exp(E_d(x) ./ (x.*k)))).\1;
T = logspace(-5, 5);
conc = subs(n, {x}, {T});
semilogy(T.\1, conc);The calculations are made for silicon. I really don't know why I can't get this right.