Calculate linear charge density of rod & mag. of E-field at point

[mhrob24]

Homework Statement

Non-conducting rod of length L = 8.15 cm has charge q= -4.23 fC uniformly distributed along its length. Calculate the linear charge density and find the magnitude of the electric field at point P, a distance of 12 cm to the right of the rod.

Relevant Equations

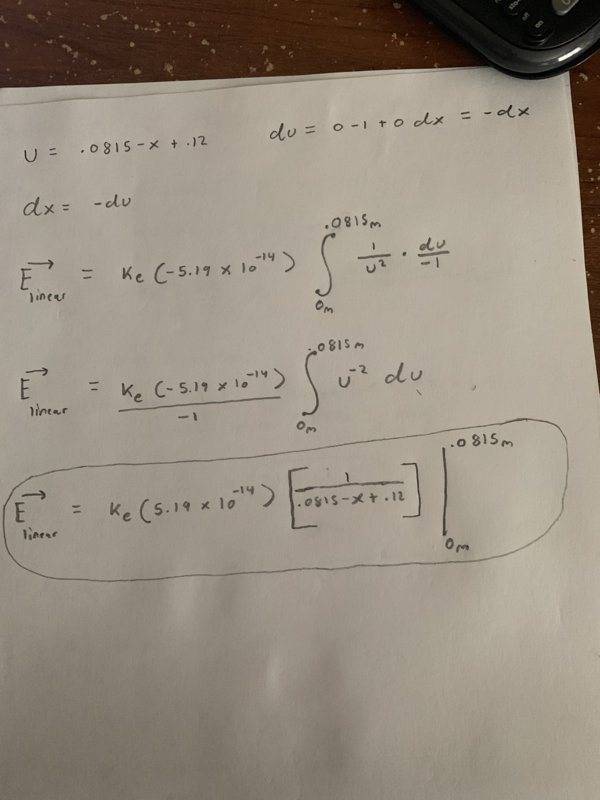
E(linear) = Ke ∫ dq/r^2 , where dq=λdl

Here is my work done for this problem, along with a diagram of the situation. I'm not worried so much about the arithmetic because our tests are only 50 min long so the problems they give us do not require heavy integration or calculus, but you need to know what goes where in the formula. That being said, I'm more concerned with knowing whether or not I have the right understanding of how to solve this problem and if I used the right tools in the correct way in order to solve it. To make it quicker for anyone attempting to help me, I would check to make sure I plugged in the correct value for my "r^2" term in the integral (distance from source of E-field to point). That is where I believe I might have made a mistake if I made one. My thinking is that the integration here is breaking down the charged rod into extremely tiny individual chunks of charge and calculating the field felt at point (P) by each chunk, then adding it up. Therefore, as you take the electric field calculation for each chunk, the distance from the chunk of charge to point (P) will be changing. If the total length of the rod is L= .0815 m, and (P) is .12m away from the right end of the rod, then we can write an equation for the distance from point (P) to each chunk of charge on the rod as a function of x (x = the distance you are at along the rod) : r = .0815m - x + .12m

Thanks in advance! (PS: my final answers are circled)

 

[haruspex]

It's basically right, but your notation is a bit off.
It's a single integral, so it makes no sense to write da and dr in it. Drop the dr, then write da=λdr.
But then you change notation, using x for the variable distance and r for the fixed offset from the end of the rod.

And I very strongly urge you to get into the habit of working entirely symbolically. Resist plugging in numbers until the final step. It has many advantages.

 

[mhrob24]

Thanks for the quick response!

Yes, I get what you mean by having the dq and dr terms in the integral. I shouldn't have expressed it like that. Also, I do have a bad habit with writing down everything as I'm working through a problem. I assuming the main advantage of not plugging in numbers until you have to is so you don't make a numerical error as you're going along (forgetting a + or - sign, wrong number, etc..) because this does tend to happen to me on problems that require arithmetic

 

[haruspex]

Thanks for the quick response!

Yes, I get what you mean by having the dq and dr terms in the integral. I shouldn't have expressed it like that. Also, I do have a bad habit with writing down everything as I'm working through a problem. I assuming the main advantage of not plugging in numbers until you have to is so you don't make a numerical error as you're going along (forgetting a + or - sign, wrong number, etc..) because this does tend to happen to me on problems that require arithmetic

Many other advantages... easier for others to follow; allows checking sanity by dimensional consistency and consideration of boundary cases; avoids building up rounding errors; and in many cases less writing!