- #1
Prashant91
- 12
- 0
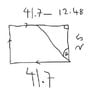
1.A aircraft leaves base and travels west at a speed of 100km/hr for 25 minutes, then turns right and travels north at a speed of 25m/s for 1000 seconds, then turns right and travels east at a speed of 75 km/hr for 10 minutes.
The plane is asked to return to base. Determine the direction that the aircraft must take to return on a direct path and describe this as a position vector.
The plane is asked to return to base. Determine the direction that the aircraft must take to return on a direct path and describe this as a position vector.