Calculate Magnetic field of wire two cavities

[JosephK]

Homework Statement

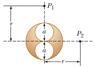
A long cylindrical conductor of radius a has two cylindrical cavities of diameter a through its entire length, as shown in cross-section in the figure below. A current I is directed out of the computer screen and is uniform through a cross section of the conductor.

(a) Provide an equation that describes the magnitude of the magnetic field in terms of µ0, I, r, and a at point P1.

Homework Equations

Biot-Savart Law

The Attempt at a Solution

I tried to calculate the magnetic field due to a solid wire at point P1. Then I calculate the magnetic field due to the top cavity at point P1 and the magnetic field of the bottom cavity at point P1. Am I on the right track?

The current density of the solid wire is J = I/A. The area A is equal (πa^2). So, the current is equal to J(πa^2). Thus the magnetic field due to the solid wire using equation B = μI/(2πr) is B = μJ(πa^2)/(2πr). Next we calculate the magnetic field due to top cavity, the distance from center of cavity to point P is r - a/2. The area of hole is (∏a^2)/4. So, J = 4I/(∏a^2). The magnetic field cavity, B1, is equal to μJ((∏a^2)/4)/(2π(r-a/2)). Now, we calculate B2, the magnetic field of cavity bottom. The distance is r + a/2, and area is same, so magnetic field is μJ((∏a^2)/4)/(2π(r+a/2)).

Then, we calculate the magnetic field of wire of two cavities. The magnetic field is B - B1 - B2. After simplifying, we obtain -μJ(a^3)(a+2)/(16(r^3-r(a^4)/4). Then the current density, is equal to I/A and the area of wire of two cavities is ∏(a^2)/2. So substituting J with (2I/(∏a^2), we obtain μI a(a+2)/(8∏r(r^2 - (a^2)/4).

 

[jbsteele]

This is the equation that describes the magnitude of the magnetic field in terms of µ0, I, r, and a at point P1.