- #1
MedEx
- 18
- 0
Homework Statement
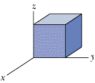
The figure shows a closed Gaussian surface in the shape of a cube of edge length 3.20 m. It lies in a region where the electric field is given by E=(1.65x+2.86)i + 4.39j + 5.47k N/C, with x in meters. What is the net charge contained by the cube?

Homework Equations
net flux= qenc/Eo (Gauss's Law)
Net flux= Ecos(theta)A
A= r^2
The Attempt at a Solution
The top, bottom and sides don't matter because they're constant, so I should only need to look at the front and back.
For the front side I had net flux = 2.86(cos (0deg))(10.24)=29.2864
For the back side I had net flux = (1.65*3.2+2.86)(cos 180deg)(10.24) = -83.3536
So the total net flux would be -54.0672.
Multiply this number by 8.55e-12 and I got the net charge to be -4.62275e-10. Any help would be appreciated.