Albert1
- 1,221
- 0
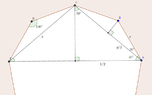
$A\,\, regular \,\,nonagon \,\,ABCDEFGHI,\,\,if \,\,\overline{AE}=1$
$find :\overline{AB}+\overline{AC}=?$
$find :\overline{AB}+\overline{AC}=?$
Last edited:
Calculate $\overline{AB}+\overline{AC}$ of Regular Nonagon ABCDEFGHI
- Topic:
- Thread starter Albert1
- Start date
-
- Tags
- Regular
Join the discussion
Registration is free. Start your own thread to ask a follow-up.
1 reply · 2K views
Discussion
lfdahl
Gold Member
MHB
- 747
- 0
My attempt:
View attachment 6451The irregular pentagon $ABCDE$ has a total interior angle sum of $540^{\circ}$. Therefore, $\angle EAB = \angle AED = 60^{\circ}$.
From the figure, we have ($x = \overline{AB}, \: \: \: y=\overline{AC}$):
\[y = \frac{1}{2\cos 40^{\circ}},\: \: \: x = \frac{y}{2\cos 20^{\circ}} = \frac{1}{4\cos 20^{\circ}\cos 40^{\circ}} \\\\ \\\\ x+y = \frac{2\cos 20^{\circ}+1}{4\cos 20^{\circ}\cos 40^{\circ}}=\frac{2\cos 20^{\circ}+1}{2(\cos 20^{\circ}+\cos 60^{\circ})} = 1.\]
From the figure, we have ($x = \overline{AB}, \: \: \: y=\overline{AC}$):
\[y = \frac{1}{2\cos 40^{\circ}},\: \: \: x = \frac{y}{2\cos 20^{\circ}} = \frac{1}{4\cos 20^{\circ}\cos 40^{\circ}} \\\\ \\\\ x+y = \frac{2\cos 20^{\circ}+1}{4\cos 20^{\circ}\cos 40^{\circ}}=\frac{2\cos 20^{\circ}+1}{2(\cos 20^{\circ}+\cos 60^{\circ})} = 1.\]
Attachments
