Calculate Skydiver's Velocity After 2 Seconds with k = 1/2 pCdA

[chengbin]

If a person has reached terminal velocity (say 50m/s), and he opens his parachute, and I want to find his speed 2 seconds after he opens his parachute, can I do this?

Solve the equation m dv/dt = mg - kv^2 and substitute k with 1/2 pCdA and substitute the value for p, Cd, and A to find velocity?

If I can, can I do this shortcut to simplify work?

The proper way of doing it would be to solve this differential equation m dv/dt = mg - kv^2 given the condition when t = 0, v = 50. But solving that would be a lot of work, and it is easy to make a mistake somewhere as my calculus skills is rusty. I can find a solution for m dv/dt = mg - kv^2 for when t = 0, v = 0 from wikipedia

http://en.wikipedia.org/wiki/Terminal_velocity

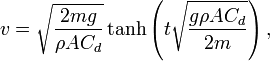
Substitute my values in, I get a number, let that be x. The velocity of a freefall object with no air resistance after 2 seconds is 9.8(2) = 19.6 m/s. The velocity slowed by drag can be found by 19.6 - x. Then I just do 50 - (19.6 - x) to get my velocity after 2 seconds.

If this doesn't work, is there a differential equation solver that will solve my equation? Thanks

 

[kuruman]

It doesn't work this way. The expression you have above is the speed as a function of time if the object starts from rest. One needs to go back to the original differential equation and solve it with the initial condition $v(t=0)=v_0$ to get a new expression for $v(t)$.

The differential equation may be written as $\frac{dv}{dt}=g-\alpha v^2$. With terminal velocity $v_T=\sqrt{g/\alpha}$, and after separation of variables, one gets$$\frac{dv}{v_T^2-v^2}=\alpha ~dt$$This can be easily integrated from $v_0$ to $v$ by separating fractions. The result is
$$v(t)=\frac{\frac{v_T+v_0}{v_T-v_0}-\exp(-2 \alpha v_T~t)}{ \frac{v_T+v_0}{v_T-v_0}+\exp(-2 \alpha v_T~t) }v_T.$$You should be able to get your expression from the above equation if you set $v_0=0$ but it's not easy to guess the form of the equation going the other way.