Calculate the charge on an oil droplet

[Shaye]

Homework Statement

A tiny negatively charged oil drop is held stationary in the electric field between two horizontal parallel plates, as shown below (please see attachment). Its mass is 4.0x10^-15kg.

Question 15,b) Use the fact that the 2 forces balance to calculate the charge on the oil drop. (g = 10 N Kg^-1).

Relevant Equations

1. F - Ma
2. E = F/Q or E = V/D (Electric field strength)

The book gives an answer of Q = 3.2 x 10^-19C

I get an answer of 6.67 x 10^-19C. Workings below:

 

[Steve4Physics]

The book gives an answer of Q = 3.2 x 10^-19C

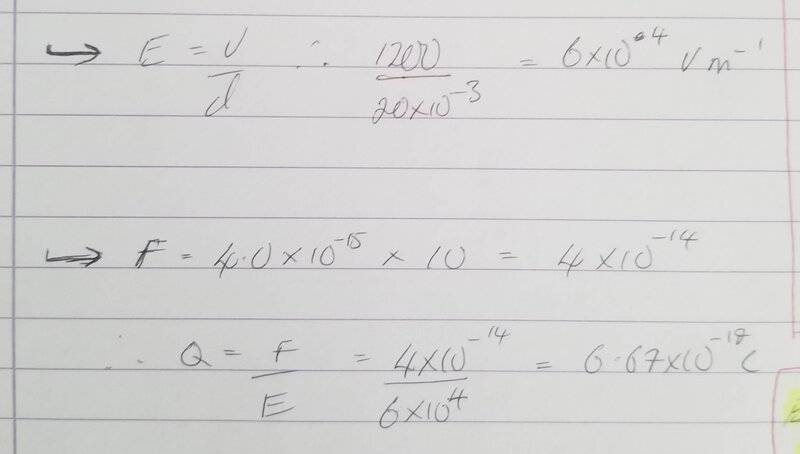
I get an answer of 6.67 x 10^-19C.

Hi @Shaye. I agree with your calculation. Looks like a mistake in the book.

Other points:
- don’t forget the minus sign for the charge;
- round the answer to 2 significant figures;
- in your intermediate step, when you find the value of the force, it’s good practice to include the unit (N);
- consider working in symbols and leaving the arithmetic to the end.

 

[PeroK]

- consider working in symbols and leaving the arithmetic to the end.

I agree. At this level, I would expect you to combine two simple formulas before plugging in the numbers:
$$Then you do that on a calculator.

 

[Shaye]

Hi @Shaye. I agree with your calculation. Looks like a mistake in the book.

Other points:
- don’t forget the minus sign for the charge;
- round the answer to 2 significant figures;
- in your intermediate step, when you find the value of the force, it’s good practice to include the unit (N);
- consider working in symbols and leaving the arithmetic to the end.

Thanks @Steve4Physics

 

[Shaye]

I agree. At this level, I would expect you to combine two simple formulas before plugging in the numbers:
$$mg = qE = \frac{qV}{d} \ \Rightarrow \ q = \frac{mgd}{V}$$Then you do that on a calculator.

Yeah I should probably start to do this going forward @PeroK Good tip!