Calculate the density of the object

[mathlearn]

View attachment 6158

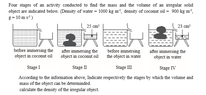
Stage II and stage IV can be used to determine as the volume of the water displaced is given.

Now how should the density be calculated :D

I know the formula for density

$density=\frac{mass}{volume}$

 

[MarkFL]

When the object is fully submerged, we can then determine its volume as given by the amount of coconut oil it displaced. We don't know it's mass though at that point. However, when it floats in the water, we know by the principle of Archimedes, that it has displaced an amount of water equal to its own mass. So, we would expect the density of the object to be greater than that of the coconut oil, but less than that of the water.

You are correct that mass density $\rho$ is given by mass $m$ per volume $V$:

$$\rho=\frac{m}{V}\tag{1}$$

which thus implies:

$$m=\rho V\tag{2}$$

So, to determine the density of the object, find its mass using the given density of water and the volume of water displaced in (2), then use this value for the mass to determine the object's density using the amount of coconut oil it displaced as its volume in (1).

 

[mathlearn]

When the object is fully submerged, we can then determine its volume as given by the amount of coconut oil it displaced. We don't know it's mass though at that point. However, when it floats in the water, we know by the principle of Archimedes, that it has displaced an amount of water equal to its own mass. So, we would expect the density of the object to be greater than that of the coconut oil, but less than that of the water.

You are correct that mass density $\rho$ is given by mass $m$ per volume $V$:

$$\rho=\frac{m}{V}\tag{1}$$

which thus implies:

$$m=\rho V\tag{2}$$

So, to determine the density of the object, find its mass using the given density of water and the volume of water displaced in (2), then use this value for the mass to determine the object's density using the amount of coconut oil it displaced as its volume in (1).

In water

$$m =1000 kg m^{-3} * 23 cm^3 \tag{2}$$
$$m =23000 kg$$

Using coconut oil

$$m =900 kg m^{-3} * 25 cm^3 \tag{2}$$
$$m = 22500 kg \tag{2}$$

Where should the acceleration due to gravity be used mentioned in the problem $g=10 ms^{-2}$

Something still looks wrong here (Thinking)

Many Thanks :)

 

[I like Serena]

In water

$$m =1000 kg m^{-3} * 23 cm^3 \tag{2}$$
$$m =23000 kg$$

Using coconut oil

$$m =900 kg m^{-3} * 25 cm^3 \tag{2}$$
$$m = 22500 kg \tag{2}$$

Where should the acceleration due to gravity be used mentioned in the problem $g=10 ms^{-2}$

Something still looks wrong here (Thinking)

Many Thanks :)

Hey mathlearn!

I think your units are a little off - those masses are on par with trucks - large trucks!

We don't need the acceleration due to gravity.
It's probably provided because Archimedes' Principle says it's the upward force on the object that is equal to the weight of the displaced fluid.
So formally we should include $g$, but it will be divided out again, so we don't need to know its value. (Nerd)

Oh, and that irregularly shaped object could almost be the votive crown of Hiero of Syracuse, which triggered Archimedes to make his discovery, yell Eureka (twice), and run naked into the streets of Syracuse. ;)

 

[mathlearn]

Hmmm a demonstration would be helpful here (Thinking)

 

[I like Serena]

Hmmm a demonstration would be helpful here (Thinking)

The volume of the votive crown (jk) is:
$$V=25 \text{ cm}^3$$
due to the results of its immersion in coconut oil.

Its mass is:
$$m = 1000 \text{ kg/m}^3 \times 23 \text{ cm}^3
= 1000 \text{ kg/m}^3 \times 23 \cdot 10^{-6} \text{ m}^3
= 23 \cdot 10^{-3} \text{ kg} = 23\text{ g}
$$
due to its immersion in water.

So the density is:
$$\rho = \frac mV = \frac{23\text{ g}}{25 \text{ cm}^3} = \frac{23}{25} \frac{\text{g}}{\text{cm}^3} = \frac{23}{25} \frac{\text{kg}}{\text{L}}$$

 

[mathlearn]

Many Thanks :) So As Mark said the density of the object was less than of water and was greater than of coconut oil slightly ;)

So to determine the volume of that votive crown it should be fully submerged in some liquid like for instance in coconut oil here ?

 

[I like Serena]

Many Thanks :) So As Mark said the density of the object was less than of water and was greater than of coconut oil slightly ;)

So to determine the volume of that votive crown it should be fully submerged in some liquid like for instance in coconut oil here ?

Yes. And if it floats, we can still measure the volume - by pushing it under. (Mmm)