evinda
Gold Member
MHB
- 3,741
- 0
Hey! (Smile)
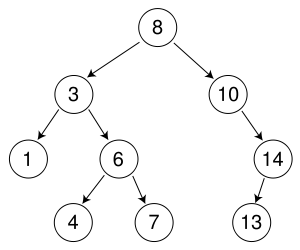
$$T=(V,E) \text{ tree }$$
$$\text{diameter of a tree } = \max_{u,v \in V} \delta(u,v)$$
$$\delta(u,v)=\text{the length of the shortest path from the vertex u to the vertex v}$$
How can we calculate the diameter of a tree,when we are given the algorithm of the Breadth-first-search ? (Wait)
According to my notes,we could do the following:
Then,the diameter of $T$ is equal to $\delta(u,w)$.
Could you explain me why we calculate the diameter in this way? (Thinking)
$$T=(V,E) \text{ tree }$$
$$\text{diameter of a tree } = \max_{u,v \in V} \delta(u,v)$$
$$\delta(u,v)=\text{the length of the shortest path from the vertex u to the vertex v}$$
How can we calculate the diameter of a tree,when we are given the algorithm of the Breadth-first-search ? (Wait)
Code:
Breadthfirstsearch(G,s)
for each u ∈ V \ {s}
color[u]<-white
d[u]<-oo
p[u]<-Ø
color[s]<-gray
d[s]<-0
p[s]<-Ø
Q<-Ø
Insert(Q,s)
while Q ≠ Ø
u<-Del(Q)
for each v ∈ Adj(u)
if color[v]=white then
color[v]<-gray
d[v]=d[u]+1
p[v]<-u
Insert(Q,v)
color[u]<-blackAccording to my notes,we could do the following:
- We implement the Breadth-first search from a given initial node $s$.
We calculate $d$ for all the vertices.
Let $u$ the vertex,such that: $$\delta(s,u)=d=\max_{v \in V} d[v]$$
[*] We implement the Breadth-first search with the vertex $u$,as the initial node.
Let $w$ the vertex,such that:
$$\delta(u,w)=d[w]=\max_{v \in V} d[v]$$
Then,the diameter of $T$ is equal to $\delta(u,w)$.
Could you explain me why we calculate the diameter in this way? (Thinking)