Calculate the exact or approximate length of one period of the wave function

[Ennio]

TL;DR Summary

exact or approximated calculation of the sinusoidal length in one period [0,2π] or corresponding to [0,λ] including the amplitude of the wave A as well as the wave number k.

The known expression of the wave function is

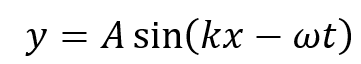
where A is the amplitude, k the wave number and ω the angular velocity.

The mathematical definition of arc length for a generical function in an interval [a,b] is

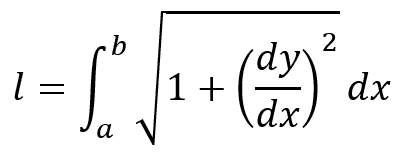
where, in our sinusoidal case:

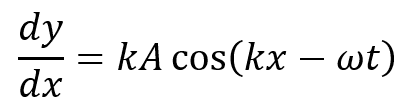
For our purpose (calculation of the length in one period [0,2π] corresponding to [0,λ]), I guess that we can remove the ωt term from the expression, so that

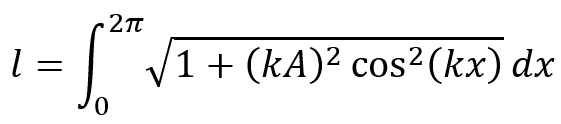
Now, I am really struggling to calculate this integral. There are some instances in internet where mathematicians calculated the length of half period [0,π] of a sinusoidal wave as

which accordingly implies

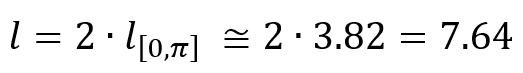
The fact is that I want to include the amplitude of the wave and the wave number by means the term

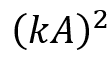as well as the wave number alone in the cos argument

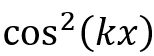in the main integral, as shown previously.

WolframAlpha and SymboLab calculates a solution involving complicated ellpitical integrals . Could you please help me in finding the right way to calculate the integral? An approximated solution would be also appreciated. The main requirement is the amplitude A and the wave number k are considered in the derivation and in the finalr result. Eventually, l has to be funtion of A and k in the final result.

Thank you in advance for your precious support.

E.

 

[malawi_glenn]

The period depends on $k$, should be pretty straightforward to figure out the $k$-dependence for the curve lenght.

Here is a plot I made for curve length with dependence of the amplitude $A$ keeping $k=1$.

What is wrong with elliptic integrals btw?

 

[Ennio]

The period depends on $k$, should be pretty straightforward to figure out the $k$-dependence for the curve lenght.

Here is a plot I made for curve length with dependence of the amplitude $A$ keeping $k=1$.
View attachment 313085

What is wrong with elliptic integrals btw?

Hi malawi_glenn. Thank you for your answer. However, what is the exact mathematical expression for the result? From your graph: if the amplitude is zero then the arc length is 3.2?

 

[malawi_glenn]

what is the exact mathematical expression for the result

Something with Elliptical functions ;)

From your graph: if the amplitude is zero then the arc length is 3.2?

Why should it be 3.2?

 

[Ennio]

It would be nice if you could share the mathematical procedure to get to the final result. Otherwise, thanks for your partial help.

 

[malawi_glenn]

It would be nice if you could share the mathematical procedure to get to the final result. Otherwise, thanks for your partial help.

And it would be nice if you could answer my questions. There are tons of information regarding approximations for elliptic integrals. Also it depends on what your application you are going to use this.

btw, is this homework?

 

[pasmith]

The arclength for a single period is $$\begin{split} \int_0^{2\pi/k} \sqrt{1 + (kA)^2\cos^2(kx)}\,dx &= 4\int_0^{\pi/(2k)} \sqrt{1 + (kA)^2\cos^2(kx)}\,dx\qquad\mbox{(by symmetry)} \\ &= 4 \sqrt{1 + (kA)^2} \int_{0}^{\pi/(2k)} \sqrt{1 - \frac{(kA)^2}{1 + (kA)^2}\sin^2(kx)}\,dx \\ &= \frac{4 \sqrt{1 + (kA)^2}}{k} \int_{0}^{\pi/2} \sqrt{1 - \frac{(kA)^2}{1 + (kA)^2}\sin^2(u)}\,du \\ &= \frac{4 \sqrt{1 + (kA)^2}}{k}E\left(\frac{kA}{\sqrt{1 + (kA)^2}}\right)\end{split}$$ where $E(y)$ is the complete elliptic integral of the second kind, which is one of those definite integrals which comes up everywhere in applications but cannot be done analytically, so we give it a name and tabulate its values numerically.

The arclength over a fraction of a quarter period can be reduced to an incomplete elliptic integral of the second kind in a similar manner: $$\int_0^{\alpha\pi/(2k)} \sqrt{1 + (kA)^2\cos^2(kx)}\,dx = \frac{\sqrt{1 + (kA)^2}}{k}E\left(\frac{\alpha\pi}{2}, \frac{kA}{\sqrt{1 + (kA)^2}}\right),\qquad 0 \leq \alpha \leq 1$$

 

[Ennio]

The arclength for a single period is $$\begin{split} \int_0^{2\pi/k} \sqrt{1 + (kA)^2\cos^2(kx)}\,dx &= 4\int_0^{\pi/(2k)} \sqrt{1 + (kA)^2\cos^2(kx)}\,dx\qquad\mbox{(by symmetry)} \\ &= 4 \sqrt{1 + (kA)^2} \int_{0}^{\pi/(2k)} \sqrt{1 - \frac{(kA)^2}{1 + (kA)^2}\sin^2(kx)}\,dx \\ &= \frac{4 \sqrt{1 + (kA)^2}}{k} \int_{0}^{\pi/2} \sqrt{1 - \frac{(kA)^2}{1 + (kA)^2}\sin^2(u)}\,du \\ &= \frac{4 \sqrt{1 + (kA)^2}}{k}E\left(\frac{kA}{\sqrt{1 + (kA)^2}}\right)\end{split}$$ where $E(y)$ is the complete elliptic integral of the second kind, which is one of those definite integrals which comes up everywhere in applications but cannot be done analytically, so we give it a name and tabulate its values numerically.

The arclength over a fraction of a quarter period can be reduced to an incomplete elliptic integral of the second kind in a similar manner: $$\int_0^{\alpha\pi/(2k)} \sqrt{1 + (kA)^2\cos^2(kx)}\,dx = \frac{\sqrt{1 + (kA)^2}}{k}E\left(\frac{\alpha\pi}{2}, \frac{kA}{\sqrt{1 + (kA)^2}}\right),\qquad 0 \leq \alpha \leq 1$$

great answer!