Calculate the focal distance of the duplicate

[Karl Karlsson]

Homework Statement

Calculate the focal distance of the duplicate

Relevant Equations

Lensmaker's equation

The picture below shows a so-called chromatic doublet, which is designed to minimize chromatic aberration, ie the wavelength dependence of the refractive index of the glass. The first lens has a flat first surface and a concave second surface with radius of curvature R and index of refraction n1 . The second lens is double convex with curvature radius R (refraction index n2) and sits close to the first lens. The lenses can be considered thin.

Calculate the focal distance of the duplicate

My try:

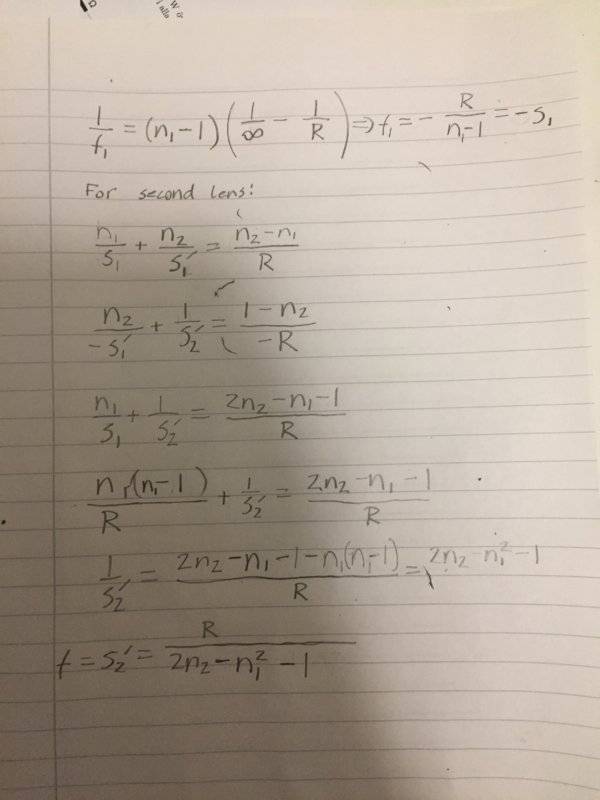
I seem to be getting the wrong answer. What am i doing wrong?

Correct answer is R/(2*n2 - n1 - 1)

 

[kuruman]

What did you use for the focal length of the second lens? Note that the figure shows a clear air gap between the two lenses. This means that you should find the two focal lengths as if the lenses were surrounded by air.

On edit: You need to adopt the standard strategy for solving compound lens problems of this kind: (a) Put an object at some finite distance $s$ in front of the combination; (b) find the position of the image $s'$; (c) Treat the image as the object for the second lens (pay close attention to what is real and what is virtual); (d) find the position of the final image $s''$; (e) let $s$ go to infinity and see what $s''$ becomes; (f) relate $s''$ to the focal length of the combination.

I tried this method for this problem and got the answer you quoted as correct.

 

[BvU]

Why does $n_1$ appear in the formula for lens 2 while $n_2$ does not appear in the formula for lens 1 ?

Does close together mean zero in between ?

 

[Karl Karlsson]

What did you use for the focal length of the second lens? Note that the figure shows a clear air gap between the two lenses. This means that you should find the two focal lengths as if the lenses were surrounded by air.

On edit: You need to adopt the standard strategy for solving compound lens problems of this kind: (a) Put an object at some finite distance $s$ in front of the combination; (b) find the position of the image $s'$; (c) Treat the image as the object for the second lens (pay close attention to what is real and what is virtual); (d) find the position of the final image $s''$; (e) let $s$ go to infinity and see what $s''$ becomes; (f) relate $s''$ to the focal length of the combination.

I tried this method for this problem and got the answer you quoted as correct.

My bad I can see my mistake as you pointed out now. I didn't think of the air gap between the lenses. Thanks!