- #1
didaw
- 27
- 0
- Homework Statement
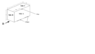
- A hinged water storage is shown below. Its top side is denoted as C, the narrow side as B and the long side as A. Assume water density is 1000 kg/m3 and gravity is 9.81 m/s2
Side A is hinged at the bottom edge and secured using a clasp at its top edge.
Dimensions are: L = 1m, H = 0.5m & W = 0.5m
a) Calculate the size and location of the water thrust force on side A
- Relevant Equations
- Area = B x D
1st moment of area = Area x 𝑦̅
Area = 1 x 0.5= 0.5
1st moment of area = 0.5 x (0.5/2) = 0.125 m
total force = p x g x 1 moment = 1000 x 9.81 x 0.125 = 1226.25N
Force = 1226.25
im pretty sure all that is right
i think the second moment = Ix = bh^3 / 3 = 1 x 0.5^3 / 3 = 0.0416
then 2nd moment of area / 1st moment of area 0.0416/0.125=0.3328
so would that mean that the location of the thrust force of 1226.25 would be 0.3328 m from the top of the box?
1st moment of area = 0.5 x (0.5/2) = 0.125 m
total force = p x g x 1 moment = 1000 x 9.81 x 0.125 = 1226.25N
Force = 1226.25
im pretty sure all that is right
i think the second moment = Ix = bh^3 / 3 = 1 x 0.5^3 / 3 = 0.0416
then 2nd moment of area / 1st moment of area 0.0416/0.125=0.3328
so would that mean that the location of the thrust force of 1226.25 would be 0.3328 m from the top of the box?