Calculate the maximum deflection of a simply supported beam

[Buzz_Lightyear]

E=220GN/m²
L= 7m
W= 20kN at 2m from the left edge.
udl=10kN/m from x=2 to x=7Beam supported in x=0 and x=7

I am not sure ir this is the way to do it.

 

[Buzz_Lightyear]

Here is my post corrected by suggestion of Chestermiller. I would like to thank him for showing me how to do it properly.

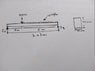
1. Homework Statement :
E=220GN/m²
L= 7m
W= 20kN at 2m from the left edge.
udl=10kN/m from x=2 to x=7
Beam supported in x=0 and x=7
width= 20mm
height=40mm

Homework Equations

$$EI\frac{\partial ²y}{\partial x²}=M$$
$$I=\frac{width\times height³}{12}$$

The Attempt at a Solution

Taking moments from R2:

$$R1\times7=20\times5+10\times5\times2,5$$
$$R1=\frac{20\times5+10\times5\times2,5}{7}=32.14kN$$
$$R2=20+50-32.14=37.86kN$$
$$EI\frac{\partial²y}{\partial x²}=32.14x-20\times(x-2)-10\times\frac{(x-2)²}{2}$$
$$EI\frac{\partial y}{\partial x}=\frac{32.14x²}{2}-\frac{20\times(x-2)²}{2}-10\times\frac{(x-2)³}{6}+A$$
$$EIy=\frac{32.14x³}{6}-\frac{20\times(x-2)³}{6}-10\times\frac{(x-2)⁴}{24}+Ax+B$$
If x=0 then y=0 then B=0
If x=7 then y=0:

$$0=\frac{32.14\times7³}{6}-\frac{20\times(7-2)³}{6}-10\times\frac{(7-2)⁴}{24}+A7$$
$$A=-165.5$$

y=max when dy/dx=0

$$0=16.07x²-10x²-40x-40-1.6666(x-2)²\times(x-2)-165.75$$
developing this equation I get:

$$0=-1.6666x³+16.05x²+20x-192.42$$

I am not very sure if this is all right. I didn't spect to get a third grade ecuation for this problem. I don't know how to continue from here

 

[Babadag]

In my opinion your calculation is correct. You have to calculate the x[third degree equation] .For instance:
https://math.vanderbilt.edu/schectex/courses/cubic/ or else
The maximum y you have for x=3.45827 m and then the deflection y=31 cm.

 

[Buzz_Lightyear]

Thank you so much. I didn't spect it to get that complicated.

 

[Chestermiller]

I don't match your moment equation. The shear force is constant at 32.14 out to x = 2. Then, the part at x > 2 kicks in.

 

[Babadag]

You are right, Chestermiller .However, since for x<=2 the maximum M(2)=64.28 kNm and for more than 2 -let's say x=3.5 M(3.5)=71.24 it seems to me you may neglect x<2 part.
The problem is to solve the cubic equation. I did it using a simply iterative program in V.B.6 but if you intend to solve it algebric you'll get always a complex number [square_root of -2916]

 

[Chestermiller]

You are right, Chestermiller .However, since for x<=2 the maximum M(2)=64.28 kNm and for more than 2 -let's say x=3.5 M(3.5)=71.24 it seems to me you may neglect x<2 part.
The problem is to solve the cubic equation. I did it using a simply iterative program in V.B.6 but if you intend to solve it algebric you'll get always a complex number [square_root of -2916]

I totally disagree with all of this. Try it both ways and see what you get. Also, a cubic equation always has one real root. Also, what does your equation predict for the moment at x = 7, where the moment is supposed to be zero?

 

[Babadag]

It is a limit on how much can suffer an electrical engineer from the mechanical static calculations. However, because no other mechanical engineer did not dare to do so I tried to start it-at least.

 

[Chestermiller]

I got x = 3.53 solving it by hand using Newton's method. This required 3 iterations.

 

[Babadag]

There are slight differences between computer calculated parameters and by hand
calculated in the last equation [post #2].
y=−1.6666x³+16.05x²+20x−192.420
If we take this equation as correct x=3.461535 y<2E-6
If x=3.53 then y=4.868>0.01 [As it could be still a good error]

 

[Chestermiller]

For the region x > 2, I get the following for the downward displacement:
$$EIy=-288.55-101.42(x-2)+32.14(x-2)^2+2.023(x-2)^3-4.167(x-2)^4$$

At x = 3.53 m, I get a downward displacement of 2.2 mm.

 

[Buzz_Lightyear]

I got x = 3.53 solving it by hand using Newton's method. This required 3 iterations.

How do you solve it using Newton's method. At college they only show us how to use Macauly's method.

 

[Nidum]

Newton's Method is a systematic procedure for finding roots of equations . It is not used in any direct way for solving structural problems - it is just useful sometimes for getting solutions to equations which can arise in structural problems .

Macaulay's Method is a systematic procedure for deriving equations for structural problems - but it does not provide any method for solving those equations .

Almost all engineering problems have the same four stages :

(a) Understanding the mechanics of the problem .
(b) Deriving the relevant equations .
(c) Solving those equations .
(d) Verifying the solution obtained .

Different methods are needed for dealing with each stage .

Just for interest - when you have a uniform beam on simple end supports and with any realistic system of unidirectional lateral loads then the point of maximum deflection is always somewhere near the mid point of the beam . This fact can be useful sometimes for finding quick solutions to certain types of problem .

 

[Nidum]

nb: Stages (a) and (b) together are commonly described as 'modelling the problem'

 

[Chestermiller]

How do you solve it using Newton's method. At college they only show us how to use Macauly's method.

Newton's method is a way of solving an equation such as f(x) = 0 for a root, x. It is iterative, and the iterative equation is:
$$x^{n+1}=x^n-\frac{f(x^n)}{f'(x^n)}$$
where $x^n$ is the value of x in the nth iteration. In the calculations I carried out, I used a finite difference approximation to $f'(x^n)$.

 

[Buzz_Lightyear]

Thank you so much for all the ideas and help. It looks that at my level I can use L/2 as the maximum deflection for practical exercises. I was overthinking about how to solve it.

 

[Chestermiller]

Thank you so much for all the ideas and help. It looks that at my level I can use L/2 as the maximum deflection for practical exercises. I was overthinking about how to solve it.

They asked for the max deflection, not just the location. Plus, you couldn't possibly have known in advance the location of the max.