Calculate the minimum uncertainty

[Kaspar]

Hello,
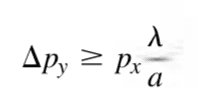
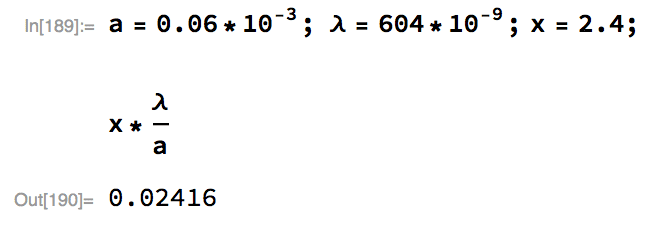
can anybody help me with solving the problem.

Homework Statement

:[/B]
Calculate minimum uncertainty?

A horizontal beam of laser light of wavelength 604 nm passes through a narrow slit that has width 0.0600 mm . The intensity of the light is measured on a vertical screen that is 2.40 m from the slit.

a.) What is the minimum uncertainty in the vertical component of the momentum of each photon in the beam after the photon has passed through the slit?
∆p_y=?

b.)Use the result of part A to estimate the width of the central diffraction maximum that is observed on the screen.
d=?

Homework Equations

and

The Attempt at a Solution

:[/B][/B]

a.) I tried using this equation and I got for ∆p_y=0.02416m
But it was wrong.

See in picture.

Can anybody help me?
Thank you.
M

 

[BvU]

Hello Kaspar,

I tried using this equation

I suppose you tried $\Delta p_y = p_x{\lambda\over a}$ ? Where does that come from ? And for $p_x$ you use the distance to the screen ?

I got for ∆p_y=0.02416 m

A $\Delta p$ with the dimension of m ?

In what context is this exercise ? Does the textbook mention uncertainty somewhere ?

 

[Kaspar]

Hello Kaspar,
I suppose you tried $\Delta p_y = p_x{\lambda\over a}$ ? Where does that come from ? And for $p_x$ you use the distance to the screen ?

Hi BvU, thanks for your reply. The equation comes from the textbook "University of Physics - Modern physics" by Zemansky (https://drive.google.com/drive/folders/13rAnc_ryXgKa3YQOXms2AGnbpFvqeXXd , book page 1268)

A $\Delta p$ with the dimension of m ?
In what context is this exercise? Does the textbook mention uncertainty somewhere ?

Yes its the chapter "38.4 WAVE–PARTICLE DUALITY, PROBABILITY, AND UNCERTAINTY"
But I still don't know how to calculate: $\Delta p_y$
Dimension should be kg*m/s .

 

[BvU]

The equation comes from the textbook "University of Physics - Modern physics" by Zemansky

Ok, but the story continues on the next page !

 

[haruspex]

And for pxpxp_x you use the distance to the screen ?

The distance to the screen cannot be relevant for part a). Isn't it just a matter of ΔyΔp_y≥ etc?

 

[Kaspar]

The distance to the screen cannot be relevant for part a). Isn't it just a matter of ΔyΔp_y≥ etc?

You are right.

I solved my problem. Here you can see. Thank you.