Calculate the minimum work to extract a body of the water

[orlan2r]

A hemisphere of 8 kg mass and 20 cm radius is at the bottom of a tank containing water. Find out the minimum work that an agent must to do to extract the hemisphere of the water.(g = 10 m/s2)

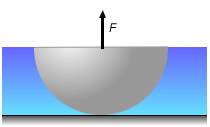
Please help me

 

[SteamKing]

Draw a free body diagram of the sphere. It would also be helpful to know the depth of the water. Id the depth the same as the radius as the figure implies?

 

[rude man]

Just posting to be notified of the progress of this thread, if any.
I notice the density of the sphere is < density of water ...

 

[orlan2r]

If the depth the same as the radius as the figure implies?

We assume that level of water is constant and inicially half of the semiesphera is inside of water.

 

[orlan2r]

I notice the density of the sphere is < density of water ...

We assume that the density of the sphere is > density of water

 

[rude man]

We assume that the density of the sphere is > density of water

That's very difficult to do:
Volume of sphere = 4/3 pi r^3 with r = 20cm → V = 33,510 cc
Mass of sphere = m = 8kg = 8000 gm
Therefore density of sphere = m/V = o.24 gm/cc whereas water density = 1 gm/cc.

This whole problem looks ridiculous.

EDIT: or maybe not: if we assume the sphere does not touch the bottom then this is actually a good problem.

 

[haruspex]

EDIT: or maybe not: if we assume the sphere does not touch the bottom then this is actually a good problem.

You don't need to make any such assumption. We're not told why it is at the bottom of the tank. Maybe it was being held down somehow.
On release, we could let it float and then lift it, but that would waste some of the potential energy. Assuming no losses, we can utilise the stored PE. That makes it a very easy calculation.

 

[haruspex]

We assume that level of water is constant and inicially half of the semiesphera is inside of water.

The depth of water cannot be constant. I think you mean the hemisphere (i.e. half the sphere were it complete) is fully immersed.

 

[orlan2r]

Volume of sphere = 4/3 pi r^3 with r = 20cm → V = 33,510 cc
Mass of sphere = m = 8kg = 8000 gm
Therefore density of sphere = m/V = o.24 gm/cc whereas water density = 1 gm/cc.

You're right rude man. Density of body < density of water. Initially the force F points down to keep submerged hemisphere.

I hope this image can help to unterstand better this problem.

 

[orlan2r]

The depth of water cannot be constant. I think you mean the hemisphere (i.e. half the sphere were it complete) is fully immersed.

The level of the surface of water is constant and at beginning the hemisphere whole is inside of the water.

 

[orlan2r]

You don't need to make any such assumption. We're not told why it is at the bottom of the tank. Maybe it was being held down somehow.
On release, we could let it float and then lift it, but that would waste some of the potential energy. Assuming no losses, we can utilise the stored PE. That makes it a very easy calculation.

Right haruspex.
Could help me in that (calculation)

 

[rl.bhat]

Net force on the hemisphere= dF = weight of the hemisphere - bouyancy force.
Assume the density of hemisphere is greater than that of the water.
The volume of the submerged part of the hemisphere is equal to V = pi/3 x h^2 x (2r - h)
Bouyancy force = V x density of water.
Total work done W = Int. dF x dh form H to zero.

 

[haruspex]

To make the surface constant height we have to assume an infinitely wide reservoir. As the hemisphere rises, the space it occupied is filled with water. Where, in effect, does that water come from? (I'm asking for a specific height within the reservoir.)

 

[rl.bhat]

To make the surface constant height we have to assume an infinitely wide reservoir. As the hemisphere rises, the space it occupied is filled with water. Where, in effect, does that water come from? (I'm asking for a specific height within the reservoir.)

In this problem, the surface of the water need not be at constant height. Bouyant force is independent of the size of the tank. If we assume the figure is correct, then the density of hemisphere is equal to the density of water. In that case it just submerses.

 

[haruspex]

In this problem, the surface of the water need not be at constant height.

You do need to assume that. If the level drops as the hemisphere rises then the buoyant force decreases faster.

 

[rl.bhat]

You do need to assume that. If the level drops as the hemisphere rises then the buoyant force decreases faster.

Since we are doing integration to find the total work done, the rate of change of depth does not matter. At any instant the buoyant force depends on the depth of the submersed portion of the hemisphere from the water surface.

 

[haruspex]

Since we are doing integration to find the total work done, the rate of change of depth does not matter. At any instant the buoyant force depends on the depth of the submersed portion of the hemisphere from the water surface.

Yes, but having raised the hemisphere a distance x, how much is still submerged? If the water level is constant it is 20cm-x, but if the tank has a finite extent the water level will have dropped and the submerged height will be less, reducing the buoyancy. As against that, it will not be necessary to raise the hemisphere 20cm to get it clear of the water. So it is not clear whether the work done will be more, the same or less. From a bit of algebra, looks to me like a falling water level requires more work to be done if, and only if, the density of the hemisphere exceeds half that of the water.

 

[rl.bhat]

Yes, but having raised the hemisphere a distance x, how much is still submerged? If the water level is constant it is 20cm-x, but if the tank has a finite extent the water level will have dropped and the submerged height will be less, reducing the buoyancy. As against that, it will not be necessary to raise the hemisphere 20cm to get it clear of the water. So it is not clear whether the work done will be more, the same or less. From a bit of algebra, looks to me like a falling water level requires more work to be done if, and only if, the density of the hemisphere exceeds half that of the water.

Yes. You are right.

 

[orlan2r]

I've resolved thus. I've using a concept called "energy potencial of pression" which is equal to pression of center gravity of body multiply for volumen of the body.
Could you verify my calculation please.

 

[haruspex]

I get the same answer by what is probably an equivalent method. Since the water level is constant, the water that flows into replace the hemisphere effectively comes from the surface of the reservoir. The average distance it falls in the process is 3R/8.

 

[orlan2r]

Thanks haruspex. Then we could say that the buoyant force is a "conservative force" and therefore we could associate to this a energy potential?

 

[haruspex]

Thanks haruspex. Then we could say that the buoyant force is a "conservative force" and therefore we could associate to this a energy potential?

Yes, it's a conservative force.