Calculate the net energy of this system (mass and Slinky in an elevator)

[leafy]

Homework Statement

Supposed we have a massless elevator as shown. Inside the elevator we have a hanging slinky and a 1kg mass attached to the slinky. We will give the elevator a initial constant speed of 1m/s upward. Then we cut the top of the slinky. The slinky is designed to fully contract in 1 second.

Relevant Equations

E=mgh

The slinky is designed to fully contract in 1 second. During this one second, the mass is weightless and move up at constant speed of 1m/s. After 1 second the mass gain 1m height in potential energy.

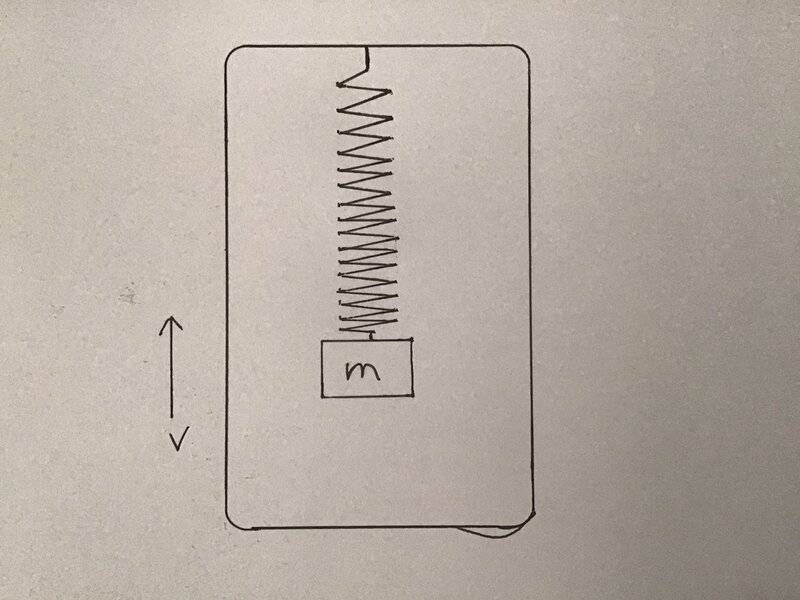Am I missing something?

 

[BvU]

During this one second, the mass is weightless

You mean something else ? $mg$ is not switched off during one second !

And, uh, what is the problem in the problem statement ? (I don't see a question there...)

$\$

 

[kuruman]

You assume, of course, that the slinky has mass. Why do you think you are missing something? Suppose you are in another elevator also moving up at constant speed of 1 m/s looking at the slinky. What would you see? Answer: What you see when you release the slinky standing on solid ground in the lab frame.

Why does it bother you that the mass is moving up at 1 m/s in the elevator picture and it doesn't bother you that the mass is temporarily at rest while the CM of the slinky accelerates as the slinky contracts in the lab frame picture?

Here is a nice video of what's going on for those unfamiliar with the falling slinky.

 

[leafy]

It bother me because I don't understand the answer.

E(initial) = E(final) ---- should be

E(initial) = 1/2mv^2 + E(slinky stretch) + E(mass linky x g x height slinky)
E(final) = (1/2mv^2 + mgh) + E(kinetic energy from slinky stretch) + E(kinetic energy from slinky height)

E(final) - E(initial) = mgh (potential energy of the mass)