Saibot
- 12
- 6
- Homework Statement
- Find resistance R if the voltmeter reading is zero in the circuit below.
- Relevant Equations
- V = IRtotal, 1/R = 1/R1 + 1/R2
The reading on the voltmeter is 0.
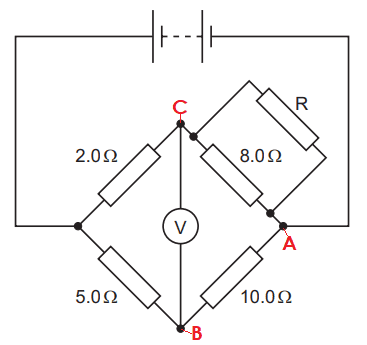
I figure the potential drop through line AB must be the same as the potential drop through AC (since voltmeter is zero). As such, the 10 Ohm resistor has the same as the effective resistance of the parallel branch.
1/10 = 1/8 + 1/R
1/R = -0.025
R = -40 Ohms
This is clearly wrong. Help please!
I figure the potential drop through line AB must be the same as the potential drop through AC (since voltmeter is zero). As such, the 10 Ohm resistor has the same as the effective resistance of the parallel branch.
1/10 = 1/8 + 1/R
1/R = -0.025
R = -40 Ohms
This is clearly wrong. Help please!