Pp122
- 1
- 3
Summary: How to calculate the equilibrium angle of a bar that is lifted on its two ends with ropes attached to fixed lifting points?
Hello and good day all,
First of all I would like to apologize in advance for my english, I am not a native speaker so some grammar errors may be left.
My question today is about the tandem lifting of an object (i.e. lifting simultaneously with two lifting devices), I would like to eventually calculate the load share in the rigging legs. I expected the question to be fairly easy but it seems way harder to solve than I thought initially, maybe that's just me though. It's been a while that I am thinking about this problem without having a clear definitive way to formulate a general answer.
Starting with the basic example of a plane problem with two lifting points of assumed known fixed coordinates connected to a simple bar via slings (able to rotate, I guess we can consider them rigid in this model) I realize that my main challenge is to find what will be the equilibrium position of the bar, after that it would be simple in-plane statics with 2 unknown forces amplitudes but known direction hence a determinate problem, nothing too difficult when this stage is reached.
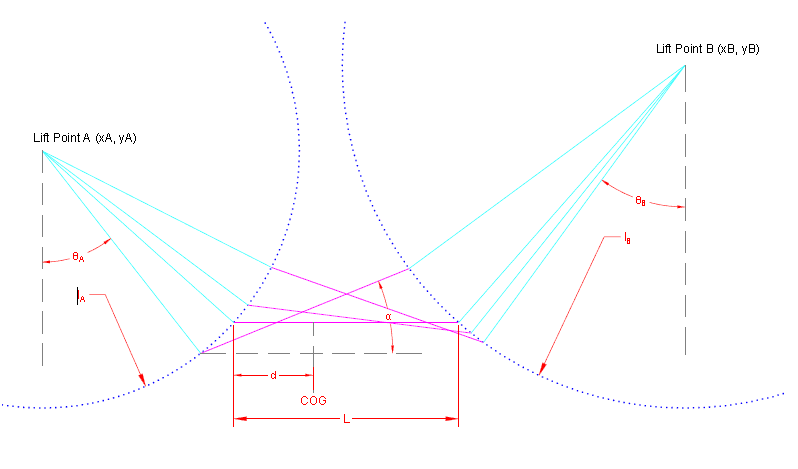
For the model, we have:
This gives:
lAsin(θA)+Lcos(α)+lBsin(θB)−(xB−xA)=0
−lAcos(θA)+Lsin(α)+lBcos(θB)−(yB−yA)=0
I have 3 unknown angles that are linked by 2 equations, my system has one degree of freedom.
The next step would be to find a physical equation or constraint to block this last DOF and determine the values of the 3 angles.
I tried to explore two ways to do so with limited success.
Hello and good day all,
First of all I would like to apologize in advance for my english, I am not a native speaker so some grammar errors may be left.
My question today is about the tandem lifting of an object (i.e. lifting simultaneously with two lifting devices), I would like to eventually calculate the load share in the rigging legs. I expected the question to be fairly easy but it seems way harder to solve than I thought initially, maybe that's just me though. It's been a while that I am thinking about this problem without having a clear definitive way to formulate a general answer.
Starting with the basic example of a plane problem with two lifting points of assumed known fixed coordinates connected to a simple bar via slings (able to rotate, I guess we can consider them rigid in this model) I realize that my main challenge is to find what will be the equilibrium position of the bar, after that it would be simple in-plane statics with 2 unknown forces amplitudes but known direction hence a determinate problem, nothing too difficult when this stage is reached.
For the model, we have:
- lA, lB lengths of the slings A and B
- L length of the bar
- d distance of the COG of the bar (0<d/L<1)
- mA, mB masses of the slings (I choose to ignore them for a start for simplicity)
- m mass of the bar
- θA, θB angles of the slings with vertical axis
This gives:
lAsin(θA)+Lcos(α)+lBsin(θB)−(xB−xA)=0
−lAcos(θA)+Lsin(α)+lBcos(θB)−(yB−yA)=0
I have 3 unknown angles that are linked by 2 equations, my system has one degree of freedom.
The next step would be to find a physical equation or constraint to block this last DOF and determine the values of the 3 angles.
I tried to explore two ways to do so with limited success.
- Use statics, rotational equilibrium gives a third equation and allows to express α in terms of θA and θB. α=arctan((1−d/L)tan(θB)−d/Ltan(θA)). Which I can simply substitue in my system. I don't really know how to solve this system precisely by hand. I had a little bit of success with this method, using a solver in excel, changing the variables θA and θB aiming to minimize the least squares for the two equations of my system. However Excel solver cannot solve the system if my lifting points are too close to each other (approaching the length of the bar). I am not really satisfied by this, if anybody could guide me to solve this system that would be much appreciated!
- There would be another option which is to express that the potential energy of the system will be minimized at equilibrium. So I would need to find the minimum for mAgyGA+mgyG+mBgyGB, so as I consider that I can neglect the masses of the slings, I would only need to find the angle α that makes the potential energy of the bar the lowest, i.e. lowest vertical position. Easier said than done! I believe that the best method for this kind of question is Newton-Raphson, that I would like to apply on yG(α)=yA−lAcos(θA)+dsin(α). I still have a term in cos(θA) therefore I still have to plug my system in the Newton-Raphson method, I don't really know how.
Attachments
Last edited by a moderator: