- #1
Junkwisch
- 31
- 0
Homework Statement
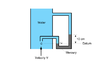
Water is flowing upwards through a vertical pipe. When a manometer is attached to the
pipe in the manner shown in the diagram, the manometer fluid (mercury) is displaced by 10
cm as illustrated.
Ignore friction in the pipe.
(i) Express the pressure at point (1a) in terms of pressure and velocity at point (1)
(ii) Calculate the velocity V of the water in the pipe.
Homework Equations
The Mechanical energy balance equation: (P2-P1)/p + 0.5*(V2^2-V1^2)+g(Z2-Z1) = 0 (no pump and friction is ignored)
Density of water 1000 kg m-3
Specific gravity of mercury 13.6
Gravitational acceleration 9.81 m s-2
The Attempt at a Solution
i) I used the mechanical energy balance equation where P2=P1a and P1=P1, since water moved upward and displaced the mercury by 10cm, I assume that V2(orV1a in this case) is equal to 0 while V1 = V, the change in height is 0.1m (the change in height between point 1 and 1a is 0)
(P1a - P1)/p -0.5*V1^2 +0.981 = 0
P1=P1a - 0.5*V1^2 + 0.981
ii) in static fluid P1 and P1a would have the same amount of pressure
By rearranging this equation, V= (2*((P1a - P1)/p + 0.981))^(1/2)
The problem I have though is how do I calculate the pressure, since in static fluid, P1a will be equal to P1, but this is not static.
*Diagram attached