Petrus
- 702
- 0
Calculate the double integral
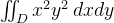 ,
,
where D is the set of all points in the first quadrant which satisfies the inequality
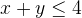 .
.
I am confused how to calculate the a,b $$\int_a^b$$ (I don't know what you call that in english)
Shall I do like this
$$y=4-x$$ and put it in the function so we get $$x^2(4-x)^2$$ and then?
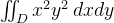
where D is the set of all points in the first quadrant which satisfies the inequality
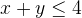
I am confused how to calculate the a,b $$\int_a^b$$ (I don't know what you call that in english)
Shall I do like this
$$y=4-x$$ and put it in the function so we get $$x^2(4-x)^2$$ and then?