Calculating accelerations in Induced Electric Fields

[Ignitia]

Homework Statement

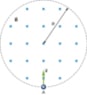
Over a region of radius R, there is a spatially uniform magnetic field B →. (See below.) At t =0, B=1.0T, after which it decreases at a constant rate to zero in 30 s.

(b) Assume that R=10.0cm. How much work is done by the electric field on a proton that is carried once clock wise around a circular path of radius 5.0 cm?

Homework Equations

W = F*d
F=q(vxB)
F=m*a

d=2πr r=5cm

The Attempt at a Solution

Since velocity and field are not given, have to go with F=m*a, but I don't see how [a] can be calculated.

with W = F*d, then W=(m*a)*(2πr)

Is there something I'm missing?

 

[kuruman]

Is there something I'm missing?

You are missing the fact that the Lorentz force ($q\vec v\times \vec B$) does no work on the proton because it is always perpendicular to $\vec v$. Besides the problem asks you to find the work done by the electric field. Where do you think that comes from?

 

[Ignitia]

You are missing the fact that the Lorentz force ($q\vec v\times \vec B$) does no work on the proton because it is always perpendicular to $\vec v$. Besides the problem asks you to find the work done by the electric field. Where do you think that comes from?

Okay, in part (a) I had calculated the Electric Field both inside and outside the magnetic field. (for reference, inside was was dB/dt * r/2 < answer checks out) If I'm reading this right, I have to take that equation, calculate the field at t = 0 and t = 30, find the difference, and multiply that by the charge of the proton?

 

[kuruman]

Okay, in part (a) I had calculated the Electric Field both inside and outside the magnetic field.

Good. The proton is in the region inside the magnetic field.

... I have to take that equation, calculate the field at t = 0 and t = 30, find the difference, and multiply that by the charge of the proton?

Is that consistent with the definition of work $W = \int \vec F \cdot d\vec s$ ? I think you should find the force on the proton (remember there is an electric field at its location) and then do the line integral.