Calculating an increasing angle in Spherical Coordinates for a curve

[Peter-]

TL;DR Summary

Using a combination of azimuthal and polar angle increases - but how?

I'm making a program that generates lines in 3D space. One feature that I need is to have an incrementally increasing angle on a line (a bending line / curve).

The problem is simple if the line exists in the xy-plane, then it would be a case of stepping say 1m, increase the azimuthal angle φ (phi) with 5 degrees, step 1m more, increase phi by an additional 5 degrees etc...

Similar, if the line exists in the zx- or zy-plane, it would be a case of increasing the polar angle θ (theta) incrementally with say 5 degrees.

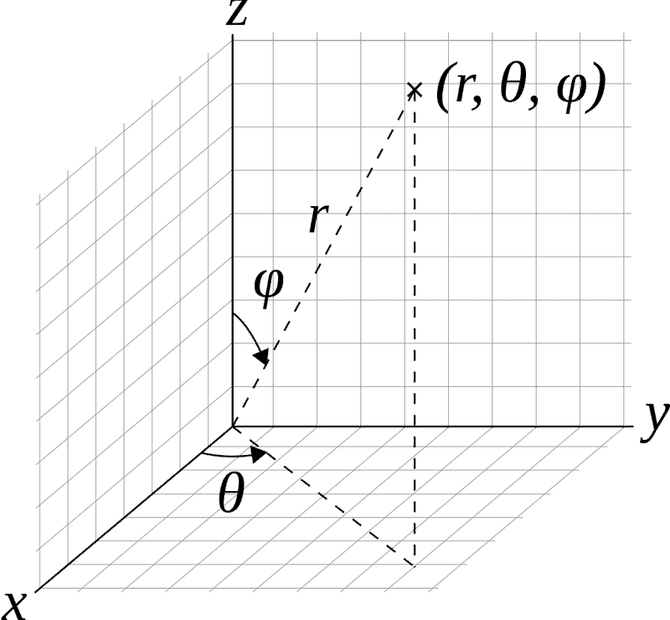
But how do I increase my line angle by say 5 degrees per 1m on a line that exist outside the planes mentioned above using a combination of azimuthal and polar angle? Let's say that I have another angle, alpha, which is the angle between the plane which my curve exists in and vertical (z), i.e. if alpha is 0 the curve will be completely vertical and if alpha is 90 degree the curve will be completely horizontal...

Any help or bright ideas getting me closer to a solution is much appreciatedKind Regards,
Peter

 

[PeroK]

I can't follow what you're trying to do. Let's say your line is along the $y$ axis, so you are at the point $P_0 = (0, y_0, 0)$. That implies a straight line from the original to $P_0$. Where are subsequent points on your curve: $P_1$, $P_2$ etc.? And why?

 

[Peter-]

It's not easy to explain the problem...

Basically what I want to make the curve below in 3d instead of 2d:

Which is basically created like this (which is a recurrent function):

                x_coordinate = (coordinate_current + math.cos(math.radians(angle_current))* length / step_resolution)
      
                y_coordinate = (coordinate_current + math.sin(math.radians(angle_current))* length / step_resolution)

I think what I have to do is to create the curve in 2D as I've been doing, and then rotate it into 3D using the techniques in this video (x-,y, and z-rotation matrices):


I really do not like spherical coordinates and I'll give the rotation matrices a go tomorrow.

Kind Regards,
Peter

 

[PeroK]

Is your motion in a 2D plane? Or, genuinely 3D?

 

[Peter-]

It’s in a plane which exists in 3D space - which is why I should be able to rotate it

 

[PeroK]

It’s in a plane which exists in 3D space - which is why I should be able to rotate it

Okay, so you can generate your curve in the x-y plane, say, and then transform that to the required plane. How do you know what the required plane is? What defines it?

 

[Peter-]

The plane will live on a line that already exists in 3D space - so the curve that I’m making is actually a branch that will spring off the existing 3D line that exists. So I’ll use the branching point and the point after it to define a vector in 3D which is parallel to the existing 3D line and then I’ll rotate my 2D curve to align with that vector and use an angle alpha which will be defined as the angle to vertical as described in my original post to help rotate the plane correctly based on some input criteria I have

 

[PeroK]

The plane will live on a line that already exists in 3D space -

That already makes little sense.

An example of a path in 2D would be a planetary orbit. It stays in a fixed plane. But, if you have two planetary orbits in different planes, then they can't both be the x-y plane. So, you'd have to define a second plane using some physical or mathematical parameters and put the second orbit in that plane.

Alternatively, a general 3D path would not stay in any plane. That path would need to be defined by some sort of formula - or perhaps iteration, like a random 3D walk. If that's what you're trying to do, then before you go any further you have to specificy how your 3D curve is defined.

 

[Peter-]

I realize that it is not easy to explain this problem, and have tried to sketch it below. Basically, I want to project my curve/branch (which is a list of 100 x-z coordinates) onto an existing line which is defined by the two point illustrated in the figure. To make it simple, let us assume that the curve/branch starts at (x0, y0, z0) which is a know point on the 3d line. To orientation the curve, we use an angle "alpha" around the axis of the 3D line from vertical (z).

Does that describe the problem better?

Kind Regards,
Peter

 

[PeroK]

But these are just generic curves. In order to write down mathematics there must be some equations describing the curves. Or, at least a description like "parabola".

 

[Peter-]

This is for a software and what I need are the rotation or project matrices.

The curve is defined as a collection of points (its will eventually become too complex to describe with a simple formula as every curvature between each point will be a probabilistic varying). The line is also clearly defined so all the necessary information is there I think..

 

[PeroK]

If we imagine that the original line is the z-axis. At some point $(0, 0, z_1)$ the first branch occurs into some 2D plane at a random angle $\theta_1$ in the x-y plane. If, for example, $\theta_1 = \frac \pi 4$, then the plane is defined by the z-axis and the line $(1, 1, 0)$. In general, the plane would be defined by the unit vectors $(0,0, 1)$ and $(\cos \theta_1, \sin \theta_1, 0)$.

Then, at subsequent points $(0, 0, z_m)$ a branch occurs into the plane defined by $(0, 0, 1)$ and $(\cos \theta_m, \sin \theta_m, 0)$.

Is that what you want? Assuming the original line is the z-axis, for example.

 

[Peter-]

Ok, let us imagine that we have a plane which is formed by the 3 points:

1. (x0, y0, z0)
2. (x1, y1, z1)
3. (x1, y1, z1+k),

where k is a number > 0. This plane now goes through all the points of the 3D line and is vertical.

Now, I want to project my curve onto that plane such that my x-axis from the 2D curve lies on top of the 3d line within the plane.

Finally, I can now use an angle "alpha" to rotate my plane (which is currently vertical) around the axis of the 3D line. So if alpha is pi/2 then the plane will become somewhat horizontal...

Does that makes sense?

 

[PeroK]

Ok, let us imagine that we have a plane which is formed by the 3 points:

1. (x0, y0, z0)
2. (x1, y1, z1)
3. (x1, y1, z1+k),

where k is a number > 0. This plane now goes through all the points of the 3D line and is vertical.

Now, I want to project my curve onto that plane such that my x-axis from the 2D curve lies on top of the 3d line within the plane.

Finally, I can now use an angle "alpha" to rotate my plane (which is currently vertical) around the axis of the 3D line. So if alpha is pi/2 then the plane will become somewhat horizontal...

Does that makes sense?

Possibly, but it's not very precise. I suggest it's easier if you describe what you want to do using the z-axis first, starting at the origin. Then, once you know what you're doing mathematically in that case, you can map that solution to the general case.

My description above was based on those diagrams you posted.

I suggest a two step process: describe the curve generation in the simplest coordinates; then map that solution to a general point and orientation.

 

[Peter-]

I think your idea is a good strategy, but I think I'll be able to figure it out.

So far, I got the branch on the line - now I just need to apply the rotations.

Kind Regards,
Peter

 

[Peter-]

I'm typing this in now (https://en.wikipedia.org/wiki/Rotation_matrix) - and just have to think about how I calculate my yaw, pitch and roll...

Then I can rotate in my curve in the local coordinates system and project the curve onto the 3d line and global coordinate system

Any ideas on how to determine yaw, pitch and roll feel free to bring them up

 

[PeroK]

Although I don't yet totally understand what you are doing, I'm not sure Euler angles are the way to go. The branching is relative to some line, which implies a unit vector in a given direction. The base solution is where the point is the origin and that unit vector is the z-axis.

The first step is to generate the mathematics (and even the code) to do that.

The more general problem can use that as a subroutine to generate the next (presumably random) branch. The last step being to rotate and translate your branch to a general point in a general direction.

Note that if we have a unit vector $(n_x, n_y, n_y)$, then that translates nicely to $(\sin \phi \cos \theta, \sin \phi \sin \theta, \cos \phi)$. Then, what you need is a rotation of $\theta$ about the z-axis and a rotation of $\phi$ about the new y-axis.

I think that's the coordinate transformation you want, followed by a translation to the branching point.

 

[PeroK]

Although, I may be misinterpreting what you want to do.

 

[Peter-]

Note that if we have a unit vector (nx,ny,ny), then that translates nicely to (sin⁡ϕcos⁡θ,sin⁡ϕsin⁡θ,cos⁡ϕ). Then, what you need is a rotation of θ about the z-axis and a rotation of ϕ about the new y-axis.

Ok, just for me to follow your thinking here...

1. What is (sin⁡ϕcos⁡θ,sin⁡ϕsin⁡θ,cos⁡ϕ)?
2. Are ϕ, ⁡θ are the angles for the point (x0,y0,z0)?

 

[PeroK]

Ok, just for me to follow your thinking here...

1. What is (sin⁡ϕcos⁡θ,sin⁡ϕsin⁡θ,cos⁡ϕ)?
2. Are ϕ, ⁡θ are the angles for the point (x0,y0,z0)?

No. Your problem is defined by two things:

1) A point on a line in space. The point has coordinates $(x_0, y_0, z_0)$ and the line is defined by a direction, which is represented by some unit vector $\hat n = (n_x, n_y, n_z) =(\sin \phi \cos \theta, \sin \phi \sin \theta, \cos \phi)$. Where $\phi, \theta$ are the spherical angles if that vector were placed at the origin.

Note: sometimes it's simpler to deal with the vector as simply $(n_x, n_y, n_x)$ and sometimes expressing it as $(\sin \phi \cos \theta, \sin \phi \sin \theta, \cos \phi)$ is useful.

2) You want something to happen at that point, which presumably depends on not just the point but the line. All your diagrams show a curve branching off from a predefined line in some way.

Note that I'm still not sure what this branching process entails, but see below.

What I'm saying is that to try to describe or code 1) and 2) in general is too complicated. And, from both a mathematical and coding point of view, it's not very modular. You have one massively complicated process.

My suggestion is to break the problem down into two steps:

Step 1: take $(x_0, y_0, z_0) = (0,0,0)$ and $\hat n = (0, 0, 1)$. I.e. the point is the origin and the line is is the z-axis.

Describe (and code) your branching function in that simple case. This would also allow you unambiguously to define your branching process and we can see what you are trying to do.

Note that step 1 could be broken down into:

1a) Define the branching process in the x-z plane. I.e. as a function: $z = f(x)$.

1b) Then, if I've understood correctly, you want to pick a random angle - let's call it $\psi$ - and have the branch occur in a plane at angle $\psi$ to the x-z plane. In other words, the branch goes off in a plane in a random direction.

I believe you should focus on that first (or whatever you actually want to do in terms of your branching process).

Then, step two is:

2a) Re-orient your branch relative to your $\hat n$ line, as opposed to the z-axis. This would be a generic re-orientation process not specific to this problem.

2b) Translate your branching from the origin to $(x_0, y_0, z_0)$. Again (this time a simple) generic process.

However you do this, I believe you have to split your problem down into several steps like that.

 

[Peter-]

Hi PeroK

I finally got the time to work on this again and have solved it.

So, what I did was basically to use rotation matrices RxRyRz on my 3d curve.

Here is a simplified version not using tensors which is easier for you to read.

# rotation around X-axis:
        curveRotatedY = (
            math.cos(rotationAngleAroundXAxisRadians) * curveY
            - math.sin(rotationAngleAroundXAxisRadians) * curveZ
        )
        curveRotatedZ = (
            math.sin(rotationAngleAroundXAxisRadians) * curveY
            + math.cos(rotationAngleAroundXAxisRadians) * curveZ
        )
        # rotation around Y-axis:
        curveZ = curveRotatedZ

        curveRotatedX = (
            math.cos(rotationAngleAroundYAxisRadians) * curveX
            + math.sin(rotationAngleAroundYAxisRadians) * curveZ
        )
        curveRotatedZ = (
            -1 * math.sin(rotationAngleAroundYAxisRadians) * curveX
            + math.cos(rotationAngleAroundYAxisRadians) * curveZ
        )

        # rotation around z axis:

        curveX = curveRotatedX

        curveRotatedX = (
            math.cos(rotationAngleAroundZAxisRadians) * curveX
            - math.sin(rotationAngleAroundZAxisRadians) * curveY
        )
        curveRotatedY = (
            math.sin(rotationAngleAroundZAxisRadians) * curveX
            + math.cos(rotationAngleAroundZAxisRadians) * curveY
        )

The rotation angles are calculated using arctan2 with some additional logic.

Although none of the input you provided was of any value, I still want to thank you for your support and it at least feels good when someone else is there to support

Kind Regards,
Peter

 

[Peter-]