- #1
Wigglyben
- 3
- 0
I'm just trying to review for an exam and the only thing I don't really get is how to calculate centers of mass. I'll just use two problems I had in my homework that I didn't know how to do. I feel like these two problems should be really easy but I have idea how to do them.
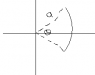
1. Find the center of mass of a uniform wire that subtends an arc θ if the radius of the arc is a. My terrible MSPaint picture to give you an idea:

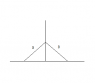
2. Find the center of mass of this isoceles triangle:

1/M [Integral] rdm
In the first one I tried to use polar coordinates and substitute dm for density*dθ. Density would be M/θ. But when you get to the integral it's 1/θ so you would get the natural log of zero or a negative number depending on how you want to do it.
For the second one, I have no idea where to begin even. Would you have to do a double integral and find the equation of the line that forms the triangle or is there an easier way?
Homework Statement
1. Find the center of mass of a uniform wire that subtends an arc θ if the radius of the arc is a. My terrible MSPaint picture to give you an idea:
2. Find the center of mass of this isoceles triangle:
Homework Equations
1/M [Integral] rdm
The Attempt at a Solution
In the first one I tried to use polar coordinates and substitute dm for density*dθ. Density would be M/θ. But when you get to the integral it's 1/θ so you would get the natural log of zero or a negative number depending on how you want to do it.
For the second one, I have no idea where to begin even. Would you have to do a double integral and find the equation of the line that forms the triangle or is there an easier way?