- #1
Karl Karlsson
- 104
- 12
- Homework Statement
- Consider a circular solenoid with length L and radius R. The solenoid is wound with n revolutions per unit length and is traversed by a current ##I_0##. If the solenoid is tightly wound (ie, n is large), the current density can be approximated by a surface current of the form ##d\vec I = I_0n\vec e_3\times d\vec S##.
The magnetic force ##d\vec F## from an external magnetic field ##\vec B## on a small surface element is given by ##d\vec F = d\vec I\times \vec B##
i) Motivate and write down a parameterization of the surface occupied by the solenoid. (Start by placing the solenoid in an appropriately selected way in a Cartesian coordinate system.) Specify in particular how the Cartesian coordinates depend on your parameters and which parameter values are allowed.
ii) Calculate the surface element ##d\vec S## in your parameterization.
iii) The solenoid is placed in an arbitrary constant magnetic field ##\vec B##. Write down the expression for dF and simplify this as far as possible.
iiii) The total moment of force on the solenoid relative to a position ##\vec x_0## is obtained by integrating ##\vec T = \int_S (\vec x - \vec x_0 )\times d\vec F## over the entire solenoid surface S. Calculate this integral for the situation described in iii) when ##\vec x_0## is the center of the solenoid.
- Relevant Equations
- ##d\vec I = I_0n\vec e_3\times d\vec S##
##d\vec F = d\vec I\times \vec B##
##\vec T = \int_S (\vec x - \vec x_0 )\times d\vec F##
i) I approximate the solenoid as a cylinder with height L and radius R. I am not sure how I am supposed to place the solenoid in the coordinate system but I think it must be like this, right?
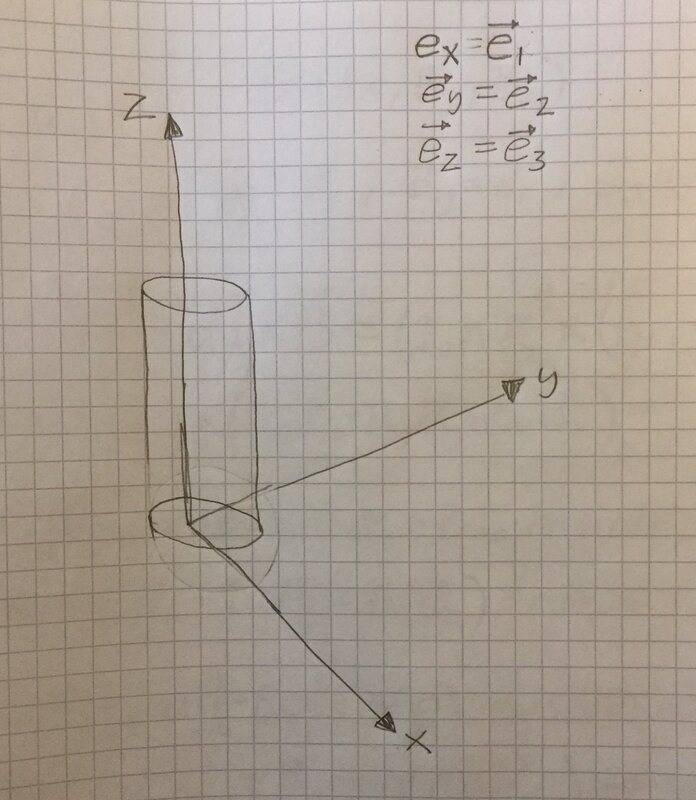
The surface occupied by the cylinder can be described by all vectors ##\vec x =(x,y,z)## so that ##x^2+y^2=R^2## , 0 ≤ z ≤ L. One parametrization to this could be ##x(t) = R\cdot cos(t), y(t)=R\cdot sin(t)## , 0 ≤ z ≤ L , 0≤t ≤ ##2\pi## , t = 0 at the x-axis and positive rotation is counterclockvise around the z axis. ##\vec x = (R\cdot cos(t), R\cdot sin(t), z)##
ii) I get ##d\vec S = \frac {d\vec x} {dt}\times \frac {d\vec x} {dz} \cdot dzdt = (R\cdot cos(t), R\cdot sin(t), 0) \cdot dzdt##. Do you get the same and is this correct?
iii) From here the expressions get so long that I will post a picture with what I wrote by hand and I wrote ρ instead of t while doing the calculations below so t = ρ
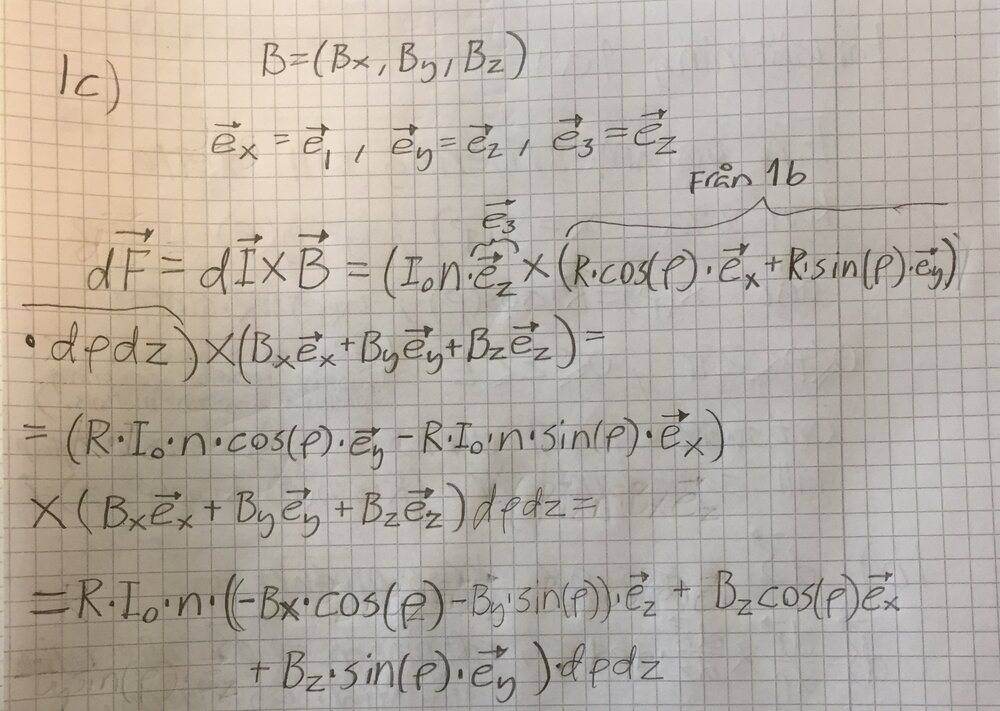
Is there any faster way to get to the result above?
iiii) Here the calculations will be even longer. If I insert the expression i got in iii) above in the integral in iiii) as the picture below shows, then I get a long expression
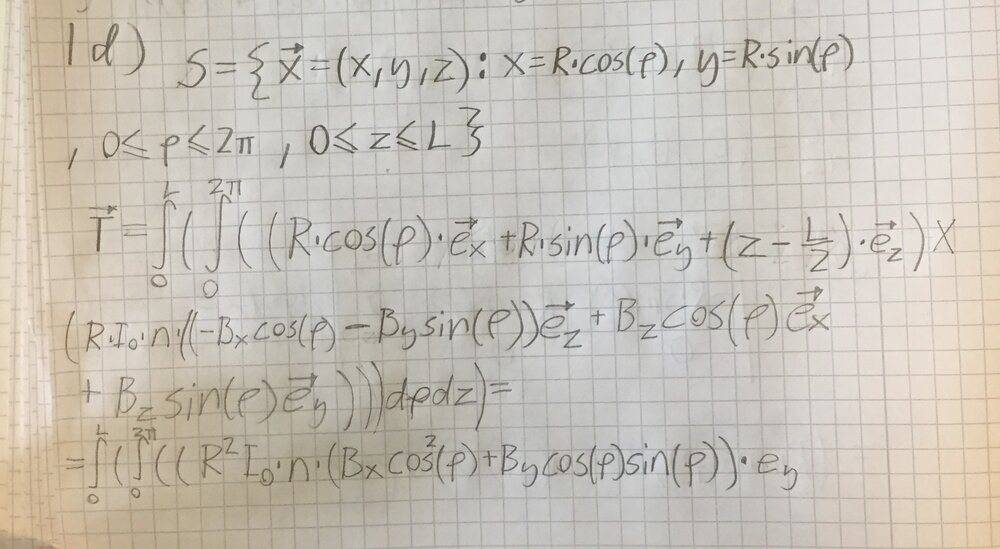
So as you can see I only started calculating the vectorproduct within the integral above until I had a feeling this is not the fastest way of solving this problem and maybe iii) as well? But how else are you supposed to do it?
Thanks in advance!
The surface occupied by the cylinder can be described by all vectors ##\vec x =(x,y,z)## so that ##x^2+y^2=R^2## , 0 ≤ z ≤ L. One parametrization to this could be ##x(t) = R\cdot cos(t), y(t)=R\cdot sin(t)## , 0 ≤ z ≤ L , 0≤t ≤ ##2\pi## , t = 0 at the x-axis and positive rotation is counterclockvise around the z axis. ##\vec x = (R\cdot cos(t), R\cdot sin(t), z)##
ii) I get ##d\vec S = \frac {d\vec x} {dt}\times \frac {d\vec x} {dz} \cdot dzdt = (R\cdot cos(t), R\cdot sin(t), 0) \cdot dzdt##. Do you get the same and is this correct?
iii) From here the expressions get so long that I will post a picture with what I wrote by hand and I wrote ρ instead of t while doing the calculations below so t = ρ
Is there any faster way to get to the result above?
iiii) Here the calculations will be even longer. If I insert the expression i got in iii) above in the integral in iiii) as the picture below shows, then I get a long expression
So as you can see I only started calculating the vectorproduct within the integral above until I had a feeling this is not the fastest way of solving this problem and maybe iii) as well? But how else are you supposed to do it?
Thanks in advance!