Calculating Current Induced in a Moving Loop

In summary, the problem involves a loop being pushed into a 0.20 T magnetic field at a velocity of 50 m/s. The resistance of the loop is 0.10 ohm. The equations used to solve the problem are I = E/R and E = |dmagnetic flux/dt|. The velocity is important in determining the length of the loop in the magnetic field, which is needed for calculating the magnetic flux. The problem requires finding the magnetic flux. Additional assistance may be needed for determining the loop's area and approaching the problem.
  • #1
dtesselstrom
31
0

Homework Statement


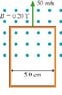
The loop in the figure is being pushed into the 0.20 T magnetic field at 50 m/s. The resistance of the loop is 0.10 ohm.


Homework Equations


I=E/R
E=|dmagnetic flux/dt|


The Attempt at a Solution


I don't know how to even start this problem all the examples give more information. I don't see what the velocity does for this problem or how to figure out the area since all they give is the width. Some help or how to approach would be much appriciated.
 

Attachments

  • knight_Figure_33_12.jpg
    knight_Figure_33_12.jpg
    6.7 KB · Views: 373
Physics news on Phys.org
  • #2
I can't see the picture yet, but I think I offer some tips.
The velocity is important as it tells you how much of the loop (and therefore area) is in the magnetic field. You get your "length" from that (it will be changing). You need that for the flux, which will be changing based on how much of the loop is in the field.
 
  • #3
What do you have to find?
 

FAQ: Calculating Current Induced in a Moving Loop

What is a moving loop and how does it relate to current induction?

A moving loop is a conducting loop that is in motion through a magnetic field. This motion induces an electric current in the loop, known as current induction.

How is the current induced in a moving loop calculated?

The current induced in a moving loop can be calculated using Faraday's law of induction, which states that the induced current is equal to the rate of change of magnetic flux through the loop. It can also be calculated using the equation V = BLv, where V is the induced voltage, B is the magnetic field strength, L is the length of the loop, and v is the velocity of the loop.

What factors affect the magnitude of the induced current in a moving loop?

The magnitude of the induced current in a moving loop is affected by the strength of the magnetic field, the speed of the loop, the size and shape of the loop, and the angle between the loop and the magnetic field.

Can the direction of the induced current in a moving loop be determined?

Yes, the direction of the induced current in a moving loop can be determined using Lenz's law, which states that the induced current will flow in a direction that opposes the change in magnetic flux through the loop.

What are some real-world applications of calculating induced current in a moving loop?

Calculating induced current in a moving loop has many practical applications, such as in generators, motors, and transformers. It is also used in technologies such as electromagnetic induction heating and magnetic levitation trains.

Similar threads

Induced Current Direction in a Changing Magnetic Field
Replies
1
Views
1K
How Does Induced Current Change with Loop Acceleration Through a Magnetic Field?
Replies
8
Views
1K
Induced EMF in a moving Loop Conductor
Replies
3
Views
2K
What is the induced magnetic force on this closed current loop?
Replies
12
Views
948
Calculate the induced EMF of a rotating loop
Replies
7
Views
2K
Induced current in two connected loops
Replies
5
Views
1K
What is the current induced in the loop when the area is π(b2 - a2)?
Replies
10
Views
1K
What happens to the current in a loop when a magnet approaches
Replies
6
Views
2K
Analyzing Bridge Circuit w/ Loop Currents
Replies
6
Views
979
How to find the maximum induced current for a diamond-shaped loop?
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top