Calculating displacement from acceleration

[mac101]

Hi All,

I have acceleration data from an accelerometer. I tried integrating it twice to calculate displacement. The problem is that its off. I am expecting about 1 cm peak to peak but instead getting about 5 cm peak to peak.

The Matlab program we use transforms the signal from a time to frequency domain then change it back after integration.

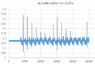
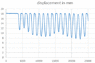
I attached a sample data set. The first column shows displacement in mm, this is the measured displacement we are trying to match. The second shows acceleration in volts. The first 3000 samples are the reading with 1 g. A change of 0.198 v causes a 1 g change.

The sampling rate is 5000 Hz.

I have been trying to figure this out for months with no luck.

Any help would be appreciated.

Thank you for your time.

 

[sophiecentaur]

Hi and welcome.

Why are you using the frequency domain for this? What motion is it that you are investigating? Why doesn't the displacement start with zero?
Some more background would be useful.
I think you need to describe what's going on before we can help. Also, a graph plot would be more easy to understand than the raw data. Few of us would be bothered to do that before giving an answer.

 

[mac101]

Thank you very much for the reply. I apologize for not putting any graphs, I should have thought about that. I added it to the file and uploaded it to this reply. Hopefully it posts.

The displacement data is captured by LVDT. The reason it doesn't start at zero is that it wasn't zeroed out. The person collecting the data forgot to do that but since we are interested in peak to peak displacements, that didn't matter.

As for what we are using this for. This is used to study chiropractic thrusts on the back of sheep. The thrusts are done mechanically by a device. Accelerometers are attached to the vertebrae and device. We are interested in calculating the displacement of the vertebrae which should be about half to 1-2 mm at the most. However, to make sure out methods are correct, we wanted to see if the displacement of the device would be similar or even in the ball park of displacements calculated from the Accelerometer attached to it and the LVDT.

As for converting it to a frequency domain. That was actually a recommendation by an engineer (that i cannot get a hold of right now), he to me there's potential for lots of error if we just integrate (that what we were originally doing) and that changing to a fluency domain would take out these issues. Having said that, I'm not expert so I cannot tell you what these exact errors are.

Again, thank you very much and I really hope someone could help me figure this out.

 

[sophiecentaur]

Perhaps the frequency domain was used for filtering out the noise.
It would not be hard to subtract a constant slope from the data, if that's all that's wrong but is it just linear? You may need also to deal with a parabolic shift from the first integration.

There are many possible reasons for a wrong scale factor. There could be places where 2pi was omitted, for instance. You would need to unpick what was done to the raw data.

 

[mac101]

First of all I would like to thank you very much for your help.

Are there particular steps to test the potential causes? I attached an image of what Matlab gives me. On the top is the acceleration data, in the middle is the velocity, and the displacement is at the bottom. The displacement is in meters so peak to peak displacement is approximately from -0.025 to 0.025 giving me a 0.05 displacement which doesn't make sense.

Again, thank you very much!