guyvsdcsniper
- 264
- 37
- Homework Statement
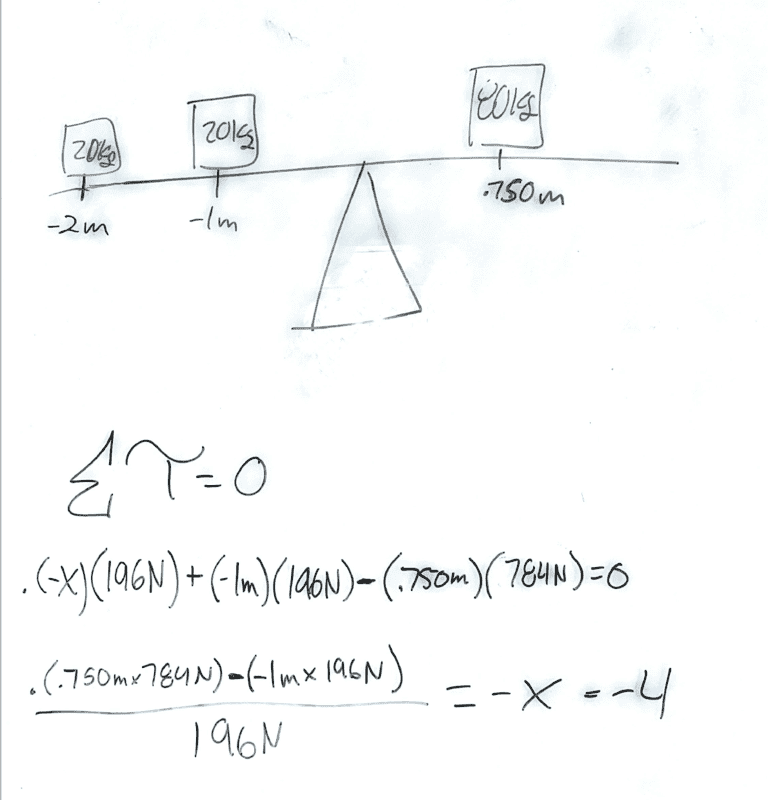
- Calculate the position of the mass m3 by using the torque balance equation.
- Relevant Equations
- ΣT=0
I am trying to find out where I need to place mass 3 to balance this see-saw. I am measuring all distances with respect to the fulcrum, so positive is to the right of the fulcrum and negative is to the left of it. Experimentally I have found the distance that mass 3 needs to be to balance this system is -2m from the fulcrum. I have set up a net torque equation and am coming up with -4m. I can see that when I subtract (.750m x 784N) by (1m x 196N) and divide by 196N I get -2m. It seems that putting (-1m) into my equation is stopping me from getting the right answer. I can't see why I would leave that value positive though if it is on the negative x-axis of the fulcrum.
Could someone help me understand where I am going wrong?

Could someone help me understand where I am going wrong?