Calculating Electric Fields and Acceleration

[StudentofPhysics]

The magnitude of each of the charges in Figure 18.21 is 9.40 10-12 C. The lengths of the sides of the rectangle are 3.00 cm and 5.00 cm. Find the magnitude of the electric field at the center of the rectangle in Figures 18.21a and 18.21b.

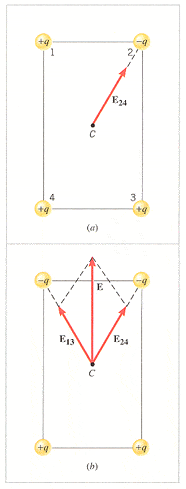
I know figure a is 198.22, but I can't seem to figure out b.



Also I'm struggling with how to tell acceleration:

A uniform electric field has a magnitude of 2.6 103 N/C. In a vacuum, a proton begins with a speed of 2.1 104 m/s and moves in the direction of this field. Find the speed of the proton after it has moved a distance of 2.0 mm.


I can't seem how to find the acceleration. The closest I can figure is that F=ma for the formula E= f/q, but there is no mass, and that formula does not include a distance so I believe it is not the one I should be using.

Any thoughts on how to do these?

 

[quantumdude]

The magnitude of each of the charges in Figure 18.21 is 9.40 10-12 C.

Before I get started, did you mean that the magnitude of the charges is $9.40\times10^{-12}C$?

 

[StudentofPhysics]

Before I get started, did you mean that the magnitude of the charges is $9.40\times10^{-12}C$?

Sorry about that. Yes, that is what I meant.

 

[quantumdude]

but I can't seem to figure out b.

You need to calculate the fields seperately, then add them like vectors. Then you can find the magnitude of the resultant. An easy way to do this is to get the magnitude of each electric field, then find a unit vector that points from the center to the charge in question. Then you can multiply the magnitude by the unit vector and voila, you have the electric field vector.

Also I'm struggling with how to tell acceleration:

A uniform electric field has a magnitude of 2.6 103 N/C. In a vacuum, a proton begins with a speed of 2.1 104 m/s and moves in the direction of this field. Find the speed of the proton after it has moved a distance of 2.0 mm.

I can't seem how to find the acceleration. The closest I can figure is that F=ma for the formula E= f/q,

So far, so good.

but there is no mass,

Ah, but there is. They tell you that the particle is a proton.

and that formula does not include a distance so I believe it is not the one I should be using.

You have to go back to kinematics here. You definitely do have a formula that relates initial position and velocity, final position and velocity, and acceleration.

 

[StudentofPhysics]

OK, proton mass I inserted but I am still struggeling.

As for adding the vectors in the first problem, I knew that and tried but it still isn't working.

 

[quantumdude]

Let's see what you've tried. Then I can tell you what's going wrong.

 

[StudentofPhysics]

Ok, for the second problem I used E=F/q. I then used F = ma to change it to E = ma/q and inserted the mass of the proton, which I looked up as equalling 1.67 x 10^-27 Kg.

but what is q? If it is the charge of a proton, which I would believe it is, then it is said to be worth 1n. I don't know how to convert that into N/C.


As for the first problem I assumed that the Fy would equal the total magnitude, (198.22 cos 45) x 2.

 

[quantumdude]

Ok, for the second problem I used E=F/q. I then used F = ma to change it to E = ma/q and inserted the mass of the proton, which I looked up as equalling 1.67 x 10^-27 Kg.

So far, so good.

but what is q? If it is the charge of a proton, which I would believe it is, then it is said to be worth 1n. I don't know how to convert that into N/C.

It is indeed the charge of the proton, which is $1.602\times10^{-19}C$. I don't understand your remark about what the charge is worth.

As for the first problem I assumed that the Fy would equal the total magnitude, (198.22 cos 45) x 2.

What's Fy?

 

[StudentofPhysics]

Fy = F in the Y direction. The Force along the x axis, Fx, will cancel out as the two forces are equal in opposite directions.

 

[StudentofPhysics]

ok, with the proton charge factored in, I've come up with a = 2.49 x 10^11what formula would I use to find the speed again?

I know its kinematics but I can't find which one.

 

[StudentofPhysics]

I would think its V =V0X (initial velocity) + a t, but what is t?

 

[quantumdude]

The problem doesn't ask for any forces. It asks for the electric field. But you are correct in saying that the horizontal components cancel.

So try to follow these steps:

1.) Calculate the magnitude of each of the 4 electric fields using:

$$E=\frac{kQ}{r^2}$$

2.) Compute the unit vectors pointing from the center to each of the 4 corners of the rectangle. Since you have correctly observed that the net electric field has no x component, it should be clear that you really only care about the y-components of these unit vectors.

3.) Multiply each E-field magnitude by its corresponding unit vector.

4.) Add them up.

5.) Find the magnitude.

 

[quantumdude]

I would think its V =V0X (initial velocity) + a t, but what is t?

No, you need the formula that doesn't refer to time. The formula you need is in the same chapter as the one you just quoted. Try to find it.

 

[StudentofPhysics]

Success! I got the second answer. Thank you very much for the help with that.


Still working on the first...

 

[quantumdude]

Super! If you get stuck again just post what you've done and we'll try to fix what's broke.

 

[MCSquare]

Hi, I'm working on a problem identical to the first question posted, and I'm on part B. I am having a whole lot of trouble figuring out what the resultant vector E is.

Here's what I've attempted thus far, oy:

a) First, I did as Mattson suggested and found the vertical components of the charges. I multiplied them by four (since the resultant is a combination of the four, right?) and my answer was incorrect.

b) Then, I did the good old 30-60-90 calculation, just because I was getting frustrated. It gave me the same answer as A, and it was incorrect.

I've done a million things and seem to end up at the same, incorrect number. I'm very frustrated, please help? Thanks.