Calculating Electric Potential and Energy in a System of Spherical Conductors

[lorenz0]

Homework Statement

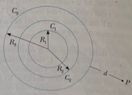
Three spherical thin and hollow conductors $C_1, C_2, C_3,$ have radii respectively $R_1, R_2, R_3.$ A charge $q_1$ is put on $C_1,$ a charge $q_2$ is put on $C_2,$ and a charge $q_3$ on $C_3.$
Find: (a) the electric field $E$ at a point $P$ at distance $d$ from $R_3;$ (b) The potential difference $V_3 -V_1$ between the conductors $C_3$ and $C_1;$ (c) Now, the conductors $C_1$ and $C_2$ are joined by a conducting cable. Find the variation in electrostatic energy energy $\Delta U_e.$

Relevant Equations

$V_3-V_1=\int_{R_3}^{R_1}\vec{E}\cdot d\vec{l},\ U=\frac{1}{2}\int \sigma V da$

(a) Using Gauss's Law $E_P=\frac{q_1+q_2+q_3}{4\pi\varepsilon_0(R_1+R_2+R_3+d)^2};(b) V_3-V_1=\int_{R_3}^{R_2}\frac{q_1+q_2}{4\pi\varepsilon_0 r^2}dr+\int_{R_2}^{R_1}\frac{q_1}{4\pi\varepsilon_0 r^2}dr=\frac{q_2}{4\pi\varepsilon_0}\left(\frac{1}{R_3}-\frac{1}{R_2}\right).$

(c) $U_i=\frac{1}{8\pi\varepsilon_0} \left(\frac{q_1^2}{R_1}+\frac{q_2^2}{R_2}+\frac{q_3^2}{R_3}\right)$ and when $C_1$ and $C_2$ are connected we have that $q_{1f}+q_{2f}=Q$, where $Q:=q_1+q_2$ and $V_1=V_2\Leftrightarrow \frac{q_1}{4\pi\varepsilon_0 R_1}=\frac{q_2}{4\pi\varepsilon_0 R_2}$ which together imply that $q_{1f}=\frac{R_1}{R_1+R_2}Q,\ q_{2f}=\frac{R_2}{R_1+R_2}Q$ so $U_f-U_i=\frac{1}{4\pi\varepsilon_0 R_1}\left(q_{1f}^2-q_1^2\right)+\frac{1}{4\pi\varepsilon_0 R_2}\left(q_{2f}^2-q_2^2\right)$

 

[TSny]

(a) Using Gauss's Law $E_P=\frac{q_1+q_2+q_3}{4\pi\varepsilon_0(R_1+R_2+R_3+d)^2}$

You are not expressing the distance from the center of the system to the field point correctly.

(b) $V_3-V_1=\int_{R_3}^{R_2}\frac{q_1+q_2}{4\pi\varepsilon_0 r^2}dr+\int_{R_2}^{R_1}\frac{q_1}{4\pi\varepsilon_0 r^2}dr=\frac{q_2}{4\pi\varepsilon_0}\left(\frac{1}{R_3}-\frac{1}{R_2}\right).$

You have set this up correctly in terms of the integrals, but your result for the evaluation of the integrals is not correct.

(c) $U_i=\frac{1}{8\pi\varepsilon_0} \left(\frac{q_1^2}{R_1}+\frac{q_2^2}{R_2}+\frac{q_3^2}{R_3}\right)$

This is not the correct expression for the initial energy of the system. Energy does not obey a superposition principle.

$\frac{1}{8\pi\varepsilon_0} \frac{q_1^2}{R_1}$ is the energy associated with conductor $C_1$ if the other conductors are not present. Similarly for the other two conductors. But, when all three conductors are present, the total energy is not the sum of these individual energies.

and when $C_1$ and $C_2$ are connected we have that $q_{1f}+q_{2f}=Q$, where $Q:=q_1+q_2$ and $V_1=V_2\Leftrightarrow \frac{q_1}{4\pi\varepsilon_0 R_1}=\frac{q_2}{4\pi\varepsilon_0 R_2}$ which together imply that $q_{1f}=\frac{R_1}{R_1+R_2}Q,\ q_{2f}=\frac{R_2}{R_1+R_2}Q$

When $C_1$ and $C_2$ are connected so that $V_1=V_2$, can there be any electric field between $C_1$ and $C_2$? What does this tell you about the final charge on $C_1$?

 

[lorenz0]

You are not expressing the distance from the center of the system to the field point correctly.
You have set this up correctly in terms of the integrals, but your result for the evaluation of the integrals is not correct.This is not the correct expression for the initial energy of the system. Energy does not obey a superposition principle.

$\frac{1}{8\pi\varepsilon_0} \frac{q_1^2}{R_1}$ is the energy associated with conductor $C_1$ if the other conductors are not present. Similarly for the other two conductors. But, when all three conductors are present, the total energy is not the sum of these individual energies.When $C_1$ and $C_2$ are connected so that $V_1=V_2$, can there be any electric field between $C_1$ and $C_2$? What does this tell you about the final charge on $C_1$?

Thanks!
For part (a) it should have been $E_P=\frac{q_1+q_2+q_3}{4\pi\varepsilon_0 (R_3+d)^2}$.
For part (b) it should have been $V_3-V_1=\frac{q_1}{4\pi\varepsilon_0}\left(\frac{1}{R_3}-\frac{1}{R_1}\right)+\frac{q_2}{4\pi\varepsilon_0}\left(\frac{1}{R_3}-\frac{1}{R_2}\right).$

For part (c) since $C_1$ and $C_2$ have the same potential the electric field between them has magnitude 0, so I was thinking that maybe the difference in energy relative to the initial situation is the one that was stored in the electric field between them, which should be $\frac{\varepsilon_0}{2}\int_{R_1}^{R_2}E^2 dV$. This approach would also have the additional benefit of not having to compute the initial and final energy, but does it make sense?

 

[kuruman]

For part (c) I think the problem is asking you to find the electrostatic energy before and after the connection is make and take the difference After - Before. By the way, there is a factor of $\frac{1}{2}$ missing in front of the integral $\varepsilon_0\int_{R_1}^{R_2}E^2 dV.$

 

[TSny]

For part (a) it should have been $E_P=\frac{q_1+q_2+q_3}{4\pi\varepsilon_0 (R_3+d)^2}$.

Yes

For part (b) it should have been $V_3-V_1=\frac{q_1}{4\pi\varepsilon_0}\left(\frac{1}{R_3}-\frac{1}{R_1}\right)+\frac{q_2}{4\pi\varepsilon_0}\left(\frac{1}{R_3}-\frac{1}{R_2}\right).$

Yes

For part (c) since $C_1$ and $C_2$ have the same potential the electric field between them has magnitude 0, so I was thinking that maybe the difference in energy relative to the initial situation is the one that was stored in the electric field between them

Sounds good.

, which should be $\varepsilon_0\int_{R_1}^{R_2}E^2 dV$.

There's a numerical factor missing here. [Edit: @kuruman already noted this.]

This approach would also have the additional benefit of not having to compute the initial and final energy, but does it make sense?

Yes, it does. Good.