- #1
VeronicaT
Dear Forum,
Please see the attached file below.
I have trouble understanding what happens at the light green gear which drives the big brown one.
I read somewhere that the force that the belt applies on the surfaces of the two pulley's is the same, so 353, 68 Nm. The torque and rpm on both pulley's is different, as is the torque.
Is it correct to say that the torque on de small gear is the same as on the big pulley? Because they are both on the same axle?
Do I calculate the force that the small gear applies on the big one like this? 53,05 Nm / 0, 037m?
Thanks for your time!
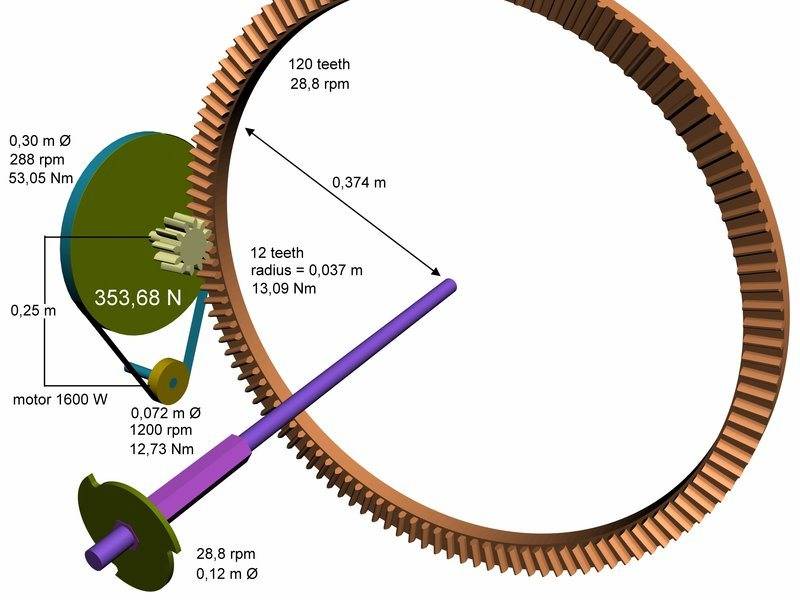
Please see the attached file below.
I have trouble understanding what happens at the light green gear which drives the big brown one.
I read somewhere that the force that the belt applies on the surfaces of the two pulley's is the same, so 353, 68 Nm. The torque and rpm on both pulley's is different, as is the torque.
Is it correct to say that the torque on de small gear is the same as on the big pulley? Because they are both on the same axle?
Do I calculate the force that the small gear applies on the big one like this? 53,05 Nm / 0, 037m?
Thanks for your time!