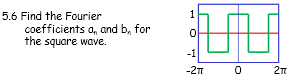Calculating Fourier Co-Efficent An of an Even Square Function

[Metalsie]

I've been trying to answer this question for several days now with no results.

Here is the question Imgur: The most awesome images on the Internet

View attachment 4935

Now, I know the answer is -4/npi, but after integrating the function piece-wise (broke it into 3 separate integrals) I got 4sin(npi/2)/npi

Here is my working Imgur: The most awesome images on the Internet

View attachment 4936

Any help or explanation is appreciated.

 

[Metalsie]

Nevermind guys, it appears that my answer is correct.

 

[MarkFL]

Nevermind guys, it appears that my answer is correct.

Your follow-up post to let us know what you found is greatly appreciated. (Yes)

 

[Metalsie]

The answer provided by the teacher (-4/npi) was basically wrong and mine was right. Sorry.

Here is the "same" problem solved

Calculating Fourier Series 1