Calculating gear ratios for a drivetrain

[Wilson123]

I'm trying to calculate the required gear sizes for the system shown below:

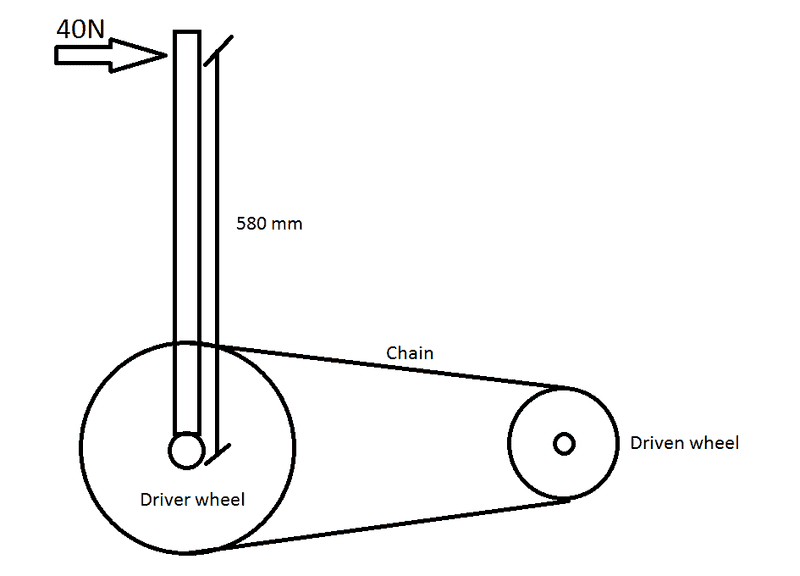
The driven wheel is connected to a 600mm diameter bicycle wheel and the driver wheel connected to a 580 mm long lever arm which has a forward driving force of 40 N.

I want to calculate the most efficient sizing of both wheels to provide the most torque to the driven wheel from the driver wheel.

To do this I think I am correct in needing to know the force which the driven wheel needs to provide to the bicycle wheel, therefore I believe the rolling resistance coefficient of the surface needs to be defined, I have found this to be 0.008 for the required terrain.

I think I have all the required information here to solve this problem however I am struggling to "connect the dots" and be provided with the sizing for both the driver wheel and driven wheel.

Any help is greatly appreciated and I will try clarify anything which is unclear if more information is needed!

 

[sandy stone]

For the most torque, with no other limitations, I think you make the driver wheel as small as possible and the driven wheel as large as possible, right?

 

[JBA]

That is correct, but I think there must be more factors to be considered than have been provided in the initial post.

 

[Wilson123]

I think I may of misunderstood how the sizing's of my gears will be... The system is for moving over rough terrain, which I presumed required high torque? However I don't want to have to incorporate different gears into the design which may be required for circumstances like setting off... Perhaps I should just go for a mid ground between the two? Allow the user to set off but also maintain an acceptable speed (a bit faster than walking speed) over rough terrain?

Can this be achieved?

 

[JBA]

Yes, you should just go for a usable mid ground gear ratio and this can be matched with the grip length positions on the handles. By gripping the top end of the handles the user can supply more torque for starting and then by moving their grip to a lower positions on the handles less torque but more speed with shorter operating strokes can be achieved with only one gear drive ratio.

 

[Wilson123]

Yes, you should just go for a usable mid ground gear ratio and this can be matched with the grip length positions on the handles. By gripping the top end of the handles the user can supply more torque for starting and then by moving their grip to a lower positions on the handles less torque but more speed with shorter operating strokes can be achieved with only one gear drive ratio.

I like your idea with the handle. What would be the best way to calculate the size of the one gear drive ratio?

 

[JBA]

For a start I suggest determining the most comfortable height on the levers for sustained operation speed of rotation of the levers by the operator and the speed of the operator's applied force, this will give you a rotation speed for the driver pulley/sprocket. Then, using the the diameter of the driven wheel and your preferred speed over the terrain, then you can calculate the required rotation speed of the driven wheel. Once you have those to rotation speeds then you can calculate the ratio between the driver and and the driven pulleys/sprockets.

 

[Wilson123]

For a start I suggest determining the most comfortable height on the levers for sustained operation speed of rotation of the levers by the operator and the speed of the operator's applied force, this will give you a rotation speed for the driver pulley/sprocket. Then, using the the diameter of the driven wheel and your preferred speed over the terrain, then you can calculate the required rotation speed of the driven wheel. Once you have those to rotation speeds then you can calculate the ratio between the driver and and the driven pulleys/sprockets.

I have the lever arm as being 690mm as being the most comfortable height.

For the speed of the operators applied force? Do you mean how many times they can exert the 40N into the lever within a given time?

The wheel diameter is 660mm with a speed of 5mph. How do I calculate the rotational speed from this?

 

[JBA]

For the speed of the operators applied force? Do you mean how many times they can exert the 40N into the lever within a given time?

The handle speed (mph) = handle strokes/min x the handle stroke length in meters x .0373 (Note: 1 meter/minute = .0373 mph)

Then: the driven pulley diameter = driver pulley diameter x (handle speed / chair speed)

Note: In my #7 post I stated that the ratio of the pulley rpms was required; but that is not necessary, the ratio of the handle speed to chair speed works just fine.

 

[Wilson123]

The handle speed (mph) = handle strokes/min x the handle stroke length in meters x .0373 (Note: 1 meter/minute = .0373 mph)

The handle stroke length being just the length of my handle (0.69m)? Also, do I need to take into account how many strokes it takes to have 1 full rotation of the gear?

 

[JBA]

No, by converting the number of strokes times the stroke length to a handle speed it is not necessary; however, if you are going to have right-left-right-left alternating arm strokes then be sure to use the (sum of the number of right and left strokes) x (each single arm stroke length) in this calculation.

 

[jack action]

If I were you, I would be considering power instead of just torque. What is the maximum power input? What is the acceptable continuous power input?

Then, you can consider scenarios with different speed and torque outputs (since power in = power out). For example, if you are at your maximum design speed, what is the output force at maximum and continuous input power? At the maximum design force, what is the output speed at maximum and continuous input power?

Once you will define the speed and force limits of your vehicle, the ratio should only be a technicality to determine.

 

[JBA]

If we were dealing with an experienced engineer, I would agree; but,I believe this individual requires a bit more than a basic "apply these basic concepts" input.

At the same time, I concede that, to this point, I have failed to address the force and work balance issues because the elements of work cannot be defined without a given resisting force and the level of rolling resistance and degrees of elevation changes over irregular terrain are going to be extremely variable with the overall average chair speed and user energy limits affected accordingly.

 

[JBA]

One side note that crossed my mind is,considering the fact that you are targeting uneven terrains and slopes, you might consider including an anti-rollback feature on your chair.

 

[sandy stone]

I think with just a little more information, we could come up with a preliminary answer to the OP's question. What do you think will be the total weight of the chair, including the operator? What is the steepest incline you expect to encounter (or negotiate)? That should determine, roughly at least, the torque required at the driven wheel and the gear ratio you need given the other dimensions you have already provided. At that point, speed will be determined by how fast and how long the operator can pump the levers at a given load (incline). I'm just curious how the torque is transmitted from the levers to the driver wheel. Are you using some kind of ratchet mechanism?

 

[Wilson123]

One side note that crossed my mind is,considering the fact that you are targeting uneven terrains and slopes, you might consider including an anti-rollback feature on your chair.

I have considered this, however it's being designed to be manufactured in a developing country, therefore I've been trying to keep the design as simple as possible. Ideally I just require the ideal sizings for these two gears to benefit from the user being able to push the levers at different heights to provide different amounts of power to the wheels. The design has a separate axle for each of the two front wheel (to allow the wheelchair to be steered), therefore alternate strokes are not an issue to consider (I don't think)

I think with just a little more information, we could come up with a preliminary answer to the OP's question. What do you think will be the total weight of the chair, including the operator? What is the steepest incline you expect to encounter (or negotiate)? That should determine, roughly at least, the torque required at the driven wheel and the gear ratio you need given the other dimensions you have already provided. At that point, speed will be determined by how fast and how long the operator can pump the levers at a given load (incline). I'm just curious how the torque is transmitted from the levers to the driver wheel. Are you using some kind of ratchet mechanism?

I am yet to exactly define the weight of the wheel chair (having some problems with my finite element analysis on my model to be sure on my tube sizing and material), however an example weight could be used for now to allow me to change this when I know? The occupants weight will be a max of 68kg. Also, the steepest incline being approximately 45 degrees?

I am using a ratchet mechanism also, the same component a bike users to allow it to freewheel so when the lever is pulled backwards, the wheel will not also move backwards.

 

[sandy stone]

45 degrees? Are you sure? That is a very steep incline, and gearing to accomplish that is going to restrict your speed. Also, I would be worried about the chair tipping over backwards. Something like a 1 in 3 incline (max) is probably more what you want, and wheelchair ramps in the US are much less than that.

 

[jack action]

Also, the steepest incline being approximately 45 degrees?

Don't even think about it. The wheel chair will not even hold itself in such an incline (not enough friction). You will be lucky to be able to climb half this steep ... and you will need a really strong person to make it move.

The steepest road in the world has a maximum slope of 21°.

 

[Wilson123]

45 degrees? Are you sure? That is a very steep incline, and gearing to accomplish that is going to restrict your speed. Also, I would be worried about the chair tipping over backwards. Something like a 1 in 3 incline (max) is probably more what you want, and wheelchair ramps in the US are much less than that.

Don't even think about it. The wheel chair will not even hold itself in such an incline (not enough friction). You will be lucky to be able to climb half this steep ... and you will need a really strong person to make it move.

The steepest road in the world has a maximum slope of 21°.

Apologies, I think I misjudged what I was suggesting... 15 degrees more suitable?

 

[JBA]

Since the plan is to have the unit operate on slopes an anti-rollback feature may be a necessity for pumping the chair up a slope (it does no good to propel the chair forward if it is going to roll back just as fast the operator can pull the handles back for the next push); and, you may be able to add the anti-rollback feature fairly simply. A possibility might be a partial spiral cam that pivots on the car frame and bears against the face of the tread of each wheel as a one way friction brake; or levers similar to the ones used as standard brakes on wheelchairs but with springs to engage them against the tires such that they act in the same manner as the above mentioned cams.

"Apologies, I think I misjudged what I was suggesting... 15 degrees more suitable?"

That may be more appropriate, particularly for off road surfaces. Hiking up any slope more than 20° can be a bit of a push even when trail hiking on foot particularly on loose soil. (Unless you are a teenager or younger, at that age you can practically hike up walls)

 

[jack action]

Apologies, I think I misjudged what I was suggesting... 15 degrees more suitable?

This is why I suggested starting with power input. This is a restriction that you have. A human can produce about 75 W (= 0.1 hp) of power continuously and can reach briefly a maximum of 1.2 hp (= 900 W). (reference 1; reference 2)

Now that you know this, you can define the speed range you want. Typical walking speed is 1.4 m/s and here you will find the running speeds by the best athletes (You probably will have to reduce those numbers by around 50 % for a typical human, so say 3 m/s).

So now we can find the forces that can be applied at tire-ground contact patch at those power and speed values (power = force X speed):

                          Walking Speed (1.4 m/s)  Running Speed (3 m/s)
Continuous Power (75 W)             53 N                   25 N
Maximum Power (900 W)              643 N                  300 N

You may decide another speed range to better suits your needs. You may find that certain force values are greater than what the wheel-ground friction can allowed. In that case, you may wish to revise your speed range. You may also define different speed ranges for different situations (For example, you may assume slower speeds for difficult terrain).

Now you know the forces (and corresponding speeds) that can be applied at the wheel. You can relate to the input force and speed to get the ratios you need for your different scenarios and then determine the one that best suits your needs.

Once you know the forces, you can convert them to an equivalent road slope or a type of difficult terrain or even a wind force if you wish. You may even make a combination of those forces. In the end, it doesn't really matter as you are stuck with the power input of human being and you cannot change that.

 

[sandy stone]

Let's see if I'm doing this right... Say the total weight of contraption plus operator is 80 kg. To lift that straight up requires (very roughly, and these are all rough estimates) 800 N. To go up a 1 in 4 slope, which is around 15 degrees, reduce the force required to 200 N. If that is applied at the rim of a 660 mm diameter wheel, then the torque required is around 66 N-m. Now the torque available from the operator is 40 N applied at the end of a 580 mm lever, or about 23 N-m. If I'm understanding the design of the contraption, then there are two levers that can be operated simultaneously, one in each hand. If that is the case, then the operator can supply around 45 N-m of torque. So in the end, a gear ratio of about 3:2 (3:1 if power is supplied on one lever only) should just allow climbing a 1 in 4 slope. Speed on level ground is going to depend a lot on rolling friction (are you on concrete? packed earth? loose dirt?) and the speed at which the operator can throw the levers back and forth. Hope that all made sense.

 

[Wilson123]

Walking Speed (1.4 m/s) Running Speed (3 m/s)
Continuous Power (75 W) 53 N 25 N
Maximum Power (900 W) 643 N 300 N

I initially stated 40N due to the British Standard for the testing of manual wheelchairs stating that 40N should not be exceeded for having a push lever, therefore I presumed this would be the only force I could take into account for calculating these wheel sizes?

You may decide another speed range to better suits your needs. You may find that certain force values are greater than what the wheel-ground friction can allowed. In that case, you may wish to revise your speed range. You may also define different speed ranges for different situations (For example, you may assume slower speeds for difficult terrain).

The wheelchair is being specifically designed for rough terrain so ideally my speeds would correspond to this.

Let's see if I'm doing this right... Say the total weight of contraption plus operator is 80 kg. To lift that straight up requires (very roughly, and these are all rough estimates) 800 N. To go up a 1 in 4 slope, which is around 15 degrees, reduce the force required to 200 N. If that is applied at the rim of a 660 mm diameter wheel, then the torque required is around 66 N-m. Now the torque available from the operator is 40 N applied at the end of a 580 mm lever, or about 23 N-m. If I'm understanding the design of the contraption, then there are two levers that can be operated simultaneously, one in each hand. If that is the case, then the operator can supply around 45 N-m of torque. So in the end, a gear ratio of about 3:2 (3:1 if power is supplied on one lever only) should just allow climbing a 1 in 4 slope. Speed on level ground is going to depend a lot on rolling friction (are you on concrete? packed earth? loose dirt?) and the speed at which the operator can throw the levers back and forth. Hope that all made sense.

This does make sense. I believe you have the idea of what I'm designing correct, the levers can operated simultaneously, one in each hand however are on separate axles. I am designing this to be used on loose dirt, I had a look into rolling resistance coefficient and believe it to be 0.008 for the surface I want (this may be wrong though).

 

[jack action]

I initially stated 40N due to the British Standard for the testing of manual wheelchairs stating that 40N should not be exceeded for having a push lever, therefore I presumed this would be the only force I could take into account for calculating these wheel sizes?

Now that you know the typical human power available, you can also estimate that the lever speed should be about 1.875 m/s (= 75 W / 40 N).

My point was that the design output force should be 53 N if the wheelchair intended speed will be 1.4 m/s. Whether you use that 53 N to climb a hill or go against a strong wind is irrelevant: It is the force that you can expect to be easily generated by your user. They can obviously use less if that is too much (like putting 10 N on the lever) and they can produce more than ten times that force for a short period of time if that is also needed (like putting 400 N on the lever). So they can always go up a higher hill if they increase the input force; But the harder the climb, the shorter will have to be the hill or your user will be out of breath before reaching the top.

Your designed wheelchair force and speed should be 53 N @ 1.4 m/s. Or, in other words, you wheelchair should be designed to handle 75 W @ 1.4 m/s (or whatever speed you think is appropriate).

If you would be designing a racing wheelchair for a 100 m I would of probably suggested 1900 W @ 10 m/s, based on running power and speed of current athletes.

 

[Wilson123]

Your designed wheelchair force and speed should be 53 N @ 1.4 m/s. Or, in other words, you wheelchair should be designed to handle 75 W @ 1.4 m/s (or whatever speed you think is appropriate).

Therefore I need a gear ratio which will convert 40N into 53N? This will then allow the chair to move at walking speed of 1.4m/s?

Does the surface which it is traveling on not have an effect on this? With it being rough terrain?

 

[JBA]

The above sounds in the right range but for travel over irregular terrain the average speed for most casual hikers is about 2+ mph (1 m/sec), admittedly this varies considerably with age and physical conditioning, which includes flat some sustained stretches of 3 mph and a large number of varied lower and higher speeds over varying terrain.

At some point, speed and time become totally irrelevant relative to simply conquering the impeding obstacle. Comparing travel over irregular terrain to a travel on a level road is like trying to compare a trip through a river rapids to a canoe trip across a smooth lake.

 

[jack action]

Does the surface which it is traveling on not have an effect on this? With it being rough terrain?

If we assume the 800 N weight stated by @sandy stone and a rolling resistance of 1% (relating to your 0.008 coefficient), that gives you a resistance of 8 N. That leaves 45 N (= 53 - 8) of "available" force. This corresponds to a 5.6% slope (= 45 / 800) or 3°, which sounds reasonable to me. Of course, the user can use more force to climb a steeper hill, he just won't be able to do it all day that's all.

If you want to consider rough terrain, well it is just a matter of considering a higher rolling resistance coefficient. With a 53 N force, that corresponds to a coefficient of 0.066 (= 53 / 800). That correspond to a stage coach (19th century) on dirt road or soft snow on road for worst case. Of course, there is no room for a slope in this case without increasing user's input effort.

If you want to consider that last case instead as your typical use, you have no choice but to reduce your designed speed. If you say the designed speed will be, for example, 0.75 m/s, then the available force will be 100 N (= 75 W / 0.75 m/s) instead of 53 N. Then you get 47 N (= 100 - 53) of "available" force which brings you back to your original leeway (but at a lower speed).

Either way, you have to find the middle ground and define your usage correctly. You won't be able to create force without reducing speed and vice versa, because you are limited by your power input. If your speed range is too wide, then you will have no choice but to use a transmission with more than one gear ratio available, like with cars or most bicycles.

 

[JBA]

As discussed above, now that you have a basic knowledge of the mechanical factors, you need to focus a bit more on refining the target users and region(s) for your unit and the actual terrain conditions they will encounter (ie the Serengeti plain or the Tibetan Mountains). You have already been focusing upon the key issue of the operator force, which is paramount because the most important question is "can this person get from point A to point B with this unit, regardless of the time involved?". The speed at which they can achieve this and the time required are secondary to that primary goal.

We, in our advanced societies have become obsessed with the speed at which we can accomplish something, where as in more remote regions and societies just being able to accomplish a task or being able to do that with a bit less effort is the most important factor.

To place this in the starkest context: "If you cannot walk, then any level of improved mobility is better than having to drag yourself across the ground or be carried everywhere."

I have worked in a jungle village region of Nigeria, West Africa a few decades ago; and I have seen this reality up close and personal, as some would put it.

 

[Work Hard Play Hard]

Sounds like a great project and you're getting some great help. After reading the thread I have some questions if you don't mind.

First I'm unsure of the lever design as described. I may have missed this but will power be delivered on both the forward and back strokes of the lever or only in one direction alternating between levers? I ask because I have no idea beyond a guess of what the better stroke is, push or pull? The pull stroke intuitively seems the more powerful stroke but the push stroke has the leverage of the chair.

"Pulley" is used in the thread and "gear" I think once. Does your design call for a pulley and belt or gear and chain? Is there any information on what's best for rough terrain?

Considering you are using a ratcheting freewheeling, I assume, hub why not use a hub with a bicycle derailleur? There are inexpensive, heavy duty mountain bike assemblies available that wouldn't add much to production complexity and would add more flexibility to the chair and possibly solve some of your gear concerns.

Finally, I've seen on racing wheelchairs that an extreme negative camber is used on the drive wheels. I assume it aids in tracking? Is there any advantage to a camber spec design for rough terrain?

 

[Wilson123]

If you want to consider that last case instead as your typical use, you have no choice but to reduce your designed speed. If you say the designed speed will be, for example, 0.75 m/s, then the available force will be 100 N (= 75 W / 0.75 m/s) instead of 53 N. Then you get 47 N (= 100 - 53) of "available" force which brings you back to your original leeway (but at a lower speed).

I don't understand how this relates back to the 0.066 rolling coefficient which you calculated from the design output force / weight of user and chair (53/800)?

I do want the design to be solely based on use over rough terrain (its what my project title indicates), therefore I want to consider the case of using the 0.066 rolling coefficient.

you need to focus a bit more on refining the target users and region(s) for your unit and the actual terrain conditions they will encounter (ie the Serengeti plain or the Tibetan Mountain

The terrain condition I intend is in rural Indonesia, therefore I am looking at dirt roads/paths with varying sized ruts and peaks.

We, in our advanced societies have become obsessed with the speed at which we can accomplish something, where as in more remote regions and societies just being able to accomplish a task or being able to do that with a bit less effort is the most important factor.

Speed is not my primary concern, as long as the system is able to travel around walking speed or perhaps a little higher I am happy. Its more just getting the gear ratio correct for use over rough terrain.

First I'm unsure of the lever design as described. I may have missed this but will power be delivered on both the forward and back strokes of the lever or only in one direction alternating between levers? I ask because I have no idea beyond a guess of what the better stroke is, push or pull? The pull stroke intuitively seems the more powerful stroke but the push stroke has the leverage of the chair.

"Pulley" is used in the thread and "gear" I think once. Does your design call for a pulley and belt or gear and chain? Is there any information on what's best for rough terrain?

Considering you are using a ratcheting freewheeling, I assume, hub why not use a hub with a bicycle derailleur? There are inexpensive, heavy duty mountain bike assemblies available that wouldn't add much to production complexity and would add more flexibility to the chair and possibly solve some of your gear concerns.

The wheels will only be driven when the levers are pushed forwards, then the freewheel mechanism allowing the levers to be pulled backwards so they can be pushed forward again.

The system will also use gears and chain, ideally taking straight from a standard second hand bike.

Unfortunately due to time constraints I now have on this project, it is better suited for to just stick to one gear ratio instead of changing the design to have multiple gears, thanks for the idea though.