Calculating Magnetic Flux: Understanding the Formula and Variables

[wr1015]

A rectangular loop of wire 24 cm by 72 cm is bent into an L shape, as shown in Figure 23-37. The magnetic field in the vicinity of the loop has a magnitude of 0.034 T and points in a direction = 22° below the y axis. The mangnetic field has no x component. Find the magnitude of the magnetic flux through the loop.

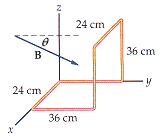
why doesn't the formula $$\phi = BA cos \theta$$ work, when A = (.36)$$^2$$, $$\theta$$ = 22, and B = .034T?? what am i missing here?

 

[Physics Monkey]

You've done the part parallel to the xz plane, so what about the xy plane? Don't just blindly use the formula, think about which parts of the loop have magnetic flux going through them.

 

[wr1015]

You've done the part parallel to the xz plane, so what about the xy plane? Don't just blindly use the formula, think about which parts of the loop have magnetic flux going through them.

don't you mean the yz plane?? the magnetic field doesn't have any x-component

 

[Physics Monkey]

No, I mean the xy plane. Why is that what I mean? Does the x component of the field have anything to do with the flux through the xy plane?

 

[wr1015]

No, I mean the xy plane. Why is that what I mean? Does the x component of the field have anything to do with the flux through the xy plane?

i don't understand what you're talking about... all i know is that if the loop is perpendicular to the field $$\theta$$ = 0 and if its parallel $$\theta$$ = 90

are you supposed to do 2 separate flux calcualtions (one for each plane) and add them accordingly?

 

[Physics Monkey]

You are going to have to do a little thinking here. I know you know more than just a formula. The flux is essentially how much field goes through the loop, right? So just by looking at your picture, can you tell if some of the field goes through the part of the loop in the xy plane. Just look and see.

 

[wr1015]

You are going to have to do a little thinking here. I know you know more than just a formula. The flux is essentially how much field goes through the loop, right? So just by looking at your picture, can you tell if some of the field goes through the part of the loop in the xy plane. Just look and see.

yes it looks like it will eventually go through the xy plane

 

[Physics Monkey]

Good. However, remember that the field is at each point in space, so "eventually" isn't really the right word. The field does go through the xy plane part of the loop.

Ok, so now that you have your picture, try using your formula. What angle is the field at relative to the normal of the xy plane? Hint: it isn't just $$\theta = 22^\circ$$, but it's related to that angle.

 

[wr1015]

Good. However, remember that the field is at each point in space, so "eventually" isn't really the right word. The field does go through the xy plane part of the loop.

Ok, so now that you have your picture, try using your formula. What angle is the field at relative to the normal of the xy plane? Hint: it isn't just $$\theta = 22^\circ$$, but it's related to that angle.

90-22 = 68.. right?

 

[Physics Monkey]

Good. Now calculate the flux through the xy plane and add it to your previous result to obtain the total flux through the loop.

 

[wr1015]

Good. Now calculate the flux through the xy plane and add it to your previous result to obtain the total flux through the loop.

so ((.034) (.36*.36) (cos 22)) + ((.034) (.24 *.36) (cos 68)) ??

 

[Physics Monkey]

Almost right. Why did you put .36*.36 for the first area? Aren't both areas the same?

Edit: I see now that you had it wrong in your first post, and I missed it. Sorry about that.

 

[wr1015]

Almost right. Why did you put .36*.36 for the first area? Aren't both areas the same?

Edit: I see now that you had it wrong in your first post, and I missed it. Sorry about that.

i see what you mean now.. thank you for your help, i really wished my book and professor would've explained this a lot better especially when dealing with different planes