Calculating Maximum Force for C1018 Steel Shaft

[JGrant]

Hello,

It's been a while since I did this in college and I cannot remember a few steps.
I am trying to calculate the maximum force my designed shaft can handle before bending/shearing.
My shaft material is C1018 steel rod, with a yield strength of 53.7 KSI and an ultimate strength of 63.8 KSI. It will be rotating at 1650 RPM with 1/11HP. The end where I would have bending is necked down to fit into another part. It has been determined that the motor shaft will be the weakest link.

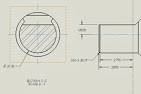
Here is a section of the shaft end. The rotating part will be in contact is the shaft over the .2795" dimension. With a force pushing down over that distance.

The area of the cross section is .06331 inches^2.

The overall shaft length is 3.527"
The shaft will be supported at .586" and 3.287" from the left.

Im mainly looking for help on how to calculate the force to bend this shaft.
If someone can just let me know how to calculate it, Id be very much appreciative.

Thank you.

 

[SteamKing]

Your thumbnail image can't be magnified. Do you have another image you can post?

 

[JGrant]

Let me know if this works.

 

[nvn]

JGrant: What is the shaft diameter before the necked down region?

 

[nvn]

JGrant: I currently assumed the shaft diameter, in the non-necked-down region, which you did not provide yet, is 9.491 mm. I currently, arbitrarily assumed a shaft endurance limit of Se = 0.45*Stu. Therefore, the maximum allowable uniformly-distributed load you can apply to the shaft necked-down region is currently w = 211 N/mm, which is a total force (applied to the necked-down region) of P = w*(7.10 mm) = 1498 N.

The governing cross section is currently at the first support, although the necked-down region currently runs a very close second. I will wait until you give us the shaft diameter, to see if it changes any outcome.

 

[JGrant]

NVN: The shaft diameter at the larger section is 9.5275 mm.
Do you calculate the force to bend the shaft the same as it is static even tho it is rotating? I thought I had to calculate a torsional force in addition to a load.

 

[nvn]

JGrant: I updated the shaft diameter to 9.5275 mm. Now w = 213.7 N/mm, which is a total force (applied to the necked-down region) of P = w*(7.10 mm) = 1517 N. The governing cross section is still at the first support. The power listed in post 1 appears to be 67.79 W, producing a shaft torque of merely Mx = 392.3 N*mm. Mx appears to be so small, that it has virtually no effect upon the above answer. I.e., inclusion of Mx only changes P to P = 1516 N. Therefore, in this particular case, it appears you can omit the torsional moment, Mx, because it has virtually no effect.

 

[JGrant]

NVN:
Thank you for helping me on this. I am feeling like I have a much better grasp on it, but I am not sure how you calculated w. (i.e. w=213.7N/mm, in post 7).
Once I know that I feel I can do these calculations on my own on any future shafts.

Thank you

 

[JGrant]

NVN:
Wouldn't the P force be located in the center of the distributed load not at the end?
Therefore, instead of using 7.1 mm, it would be 3.55mm?

Thank you for helping me with this,
Sorry if I ask to many questions.

 

[nvn]

JGrant: Yes, the P force is located at the center of the uniformly-distributed load (UDL), which is where I put it. The UDL has a length of 7.10 mm, not 3.55 mm.