- #1
Saladsamurai
- 3,020
- 7
!Help Please! Bending (stuck)
[tex]\sigma_{max}=\frac{Mc}{I}[/tex]
I am not sure where I am messing this up.
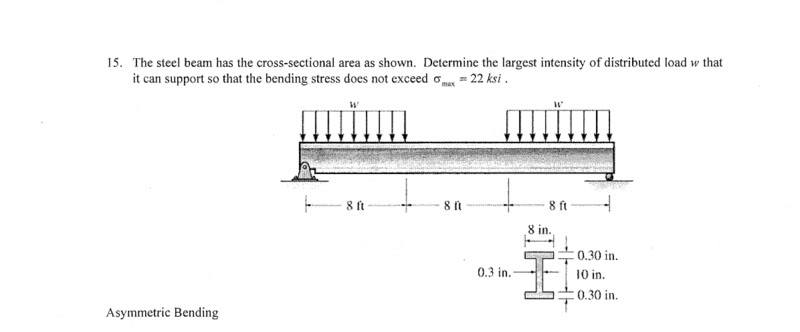
I am pretty I found I correctly to be 140.144.
But I think I am using the wrong internal force.
I am going with replacing the distributed load with a concentrated load and getting:
[tex]\sigma_{max}=\frac{4*8*w*c}{I}[/tex]
[tex]\Rightarrow w=\frac{22(10^6)(140.14)}{4*8*5.3}[/tex]
But this is off by many orders of magnitude. It is supposed to be w=1.65 kip/ft
Where am I going wrong
Homework Statement
Homework Equations
[tex]\sigma_{max}=\frac{Mc}{I}[/tex]
The Attempt at a Solution
I am not sure where I am messing this up.
I am pretty I found I correctly to be 140.144.
But I think I am using the wrong internal force.
I am going with replacing the distributed load with a concentrated load and getting:
[tex]\sigma_{max}=\frac{4*8*w*c}{I}[/tex]
[tex]\Rightarrow w=\frac{22(10^6)(140.14)}{4*8*5.3}[/tex]
But this is off by many orders of magnitude. It is supposed to be w=1.65 kip/ft
Where am I going wrong