Albert1
- 1,221
- 0
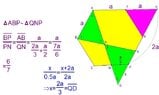
Regular hexagon $ABCDEF$,points $M$ and $N$ are midpoints of $\overline{CD}$
and $\overline {DE}$ respectively, point $P$ is the intersection of $\overline {AM}$ and $\overline{BN}$
Find $\dfrac {\overline{BP}}{\overline {PN}}$
and $\overline {DE}$ respectively, point $P$ is the intersection of $\overline {AM}$ and $\overline{BN}$
Find $\dfrac {\overline{BP}}{\overline {PN}}$