- #1
Yankel
- 395
- 0
Hello all,
I need to find the second order derivative of w by t, and to calculate it's value at t=1.
This is what I know about w, x and y.
\[w=ln(x+y)\]
\[x=e^{t}\]
\[y=e^{-t}\]The answer in the book is:
\[\frac{4}{(e^{t}+e^{-t})^{2}}\]
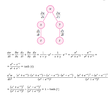
I got another answer and I don't know what I did wrong, my solution is attached as an image.
View attachment 1997
Would appreciate your help with it. Thank you.
P.S According to Maple I am correct
I need to find the second order derivative of w by t, and to calculate it's value at t=1.
This is what I know about w, x and y.
\[w=ln(x+y)\]
\[x=e^{t}\]
\[y=e^{-t}\]The answer in the book is:
\[\frac{4}{(e^{t}+e^{-t})^{2}}\]
I got another answer and I don't know what I did wrong, my solution is attached as an image.
View attachment 1997
Would appreciate your help with it. Thank you.
P.S According to Maple I am correct
Attachments
Last edited: