Calculating Self Capacitance of an Isolated Sphere

[Saitama]

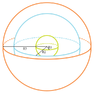
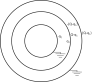
Homework Statement

(see attachment)

Homework Equations

The Attempt at a Solution

The self capacitance of an isolated sphere is $4\pi \epsilon_o R$ where R is the radius of sphere but I am not sure how to begin on this one.

Any help is appreciated. Thanks!

 

[voko]

I do not think it is correct to talk about self-capacitance here. Self-capacitance involves a potential difference with a infinitely far away object, while in this case you are given two other objects at finite distances. I think you could treat the setup as two parallel capacitors, formed by spheres 1-2 and 2-3.

 

[ehild]

Add some charge Q onto the middle sphere, find the electric field and potential in the regions between the spheres. You know that the potential is zero on the inner and outer sphere.

ehild

 

[Saitama]

I think you could treat the setup as two parallel capacitors, formed by spheres 1-2 and 2-3.

But how will that help in finding the self capacitance of the middle sphere?

Add some charge Q onto the middle sphere, find the electric field and potential in the regions between the spheres. You know that the potential is zero on the inner and outer sphere.

Electric field outside the sphere is given by $kQ/r^2$ and inside it is zero but I am still clueless. :(

 

[voko]

But how will that help in finding the self capacitance of the middle sphere?

You have ignored what I wrote earlier.

 

[Saitama]

You have ignored what I wrote earlier.

Can you please shed some more light on this? I have checked your post more than 10 times but I still can't see what I have missed.

 

[voko]

You are explicitly given potentials between three objects, with finite distances from one another. Self-capacitance, however, is defined in terms of the potential difference with an infinite-radius sphere. You can't have it both ways.

 

[Saitama]

You are explicitly given potentials between three objects, with finite distances from one another. Self-capacitance, however, is defined in terms of the potential difference with an infinite-radius sphere. You can't have it both ways.

Do you mean that the given question is wrong then?

Continuing ehild's suggestion, if I give a charge to the middle sphere, will there be any charges induced on the other spheres?

 

[ehild]

Do you mean that the given question is wrong then?

Why should it be wrong?

Continuing ehild's suggestion, if I give a charge to the middle sphere, will there be any charges induced on the other spheres?

Why not?

ehild

 

[Saitama]

Why not?

ehild

Please see the attachment if I have mentioned the induced charges properly (I think they are wrong).

If they are right, should I calculate the potential at the surface of innermost and outermost spheres and set them equal to zero?

I did these types of problems in the past but now I have completely forgotten how to do them. :(

 

[SammyS]

Please see the attachment if I have mentioned the induced charges properly (I think they are wrong).

If they are right, should I calculate the potential at the surface of innermost and outermost spheres and set them equal to zero?

I did these types of problems in the past but now I have completely forgotten how to do them. :(

That looks good to me, except for the charge on the outside of the outer sphere.

 

[Saitama]

That looks good to me, except for the charge on the outside of the outer sphere.

Yes, I too think that its wrong that's why I wrote in brackets that they look wrong to me. Any hint about what should be those charges?

 

[ehild]

Yes, I too think that its wrong that's why I wrote in brackets that they look wrong to me. Any hint about what should be those charges?

that is zero outside.

ehild

 

[SammyS]

Yes, I too think that its wrong that's why I wrote in brackets that they look wrong to me. Any hint about what should be those charges?

The potential of the sphere is zero, so the electric field exterior to the sphere must be zero.

 

[Saitama]

The potential of the sphere is zero, so the electric field exterior to the sphere must be zero.

The charges mentioned on the inner surface of outermost sphere are right?

When I calculate the potential, do I need to add potential of both outer and inner surfaces of each sphere?

 

[SammyS]

The charges mentioned on the inner surface of outermost sphere are right?

Yes. The charge on the inner surface are exactly opposite the charge on the outer surface of the middle shell.

When I calculate the potential, do I need to add potential of both outer and inner surfaces of each sphere?

No. (Assuming I understand your question correctly.)

The potential difference between the middle & outer shells should give you the charge, Q - q₁ .

The potential difference between the inner & middle shells should give you the charge, q₁ .

 

[ehild]

Apply Gauss's Law in the regions between the spheres. Integrate the electric field to get the potential difference between the middle sphere and the inner one, and also between the middle sphere and the outer one. They must be equal.

ehild

 

[Saitama]

Apply Gauss's Law in the regions between the spheres. Integrate the electric field to get the potential difference between the middle sphere and the inner one, and also between the middle sphere and the outer one. They must be equal.

ehild

The potential difference between the innermost and the middle sphere is:
kq_1 \left(\frac{1}{R_1}-\frac{1}{R_2}\right)

The potential difference between the middle sphere and the outermost sphere is:
k(Q-q_1)\left(\frac{1}{R_3}-\frac{1}{R_2}\right)

Have I calculated the potential difference right?

 

[ehild]

Check the sign of the second one.

 

[Saitama]

Check the sign of the second one.

I expected you to say that but I couldn't find the mistake in my working.
Potential at the surface of outer sphere is $k(Q-q_1)/R_3$ and potential at the surface of middle sphere is $k(Q-q_1)/R_2$, therefore the potential difference is k(Q-q_1)\left(\frac{1}{R_3}-\frac{1}{R_2}\right).

 

[ehild]

The potential of both the inner and the outer sphere is zero (with respect to infinity). Assuming positive Q, the potential of the middle sphere is positive. What is the potential of the middle sphere?
You can not write the potential in this problem as kQ/r, as it is zero both at r=R1 and r=R3.
Do what I said about the electric field.


ehild

 

[Saitama]

You can not write the potential in this problem as kQ/r, as it is zero both at r=R1 and r=R3.
Do what I said about the electric field.

The electric field between the middle sphere and the outermost sphere is $k(Q-q_1)/r^2$.
V(R_3)-V(R_2)=-\int_{R_2}^{R_3} \vec{E} \cdot \vec{dr}

$V(R_3)=0$. Hence
V(R_2)=k(Q-q_1)\left(\frac{1}{R_2}-\frac{1}{R_3}\right)

Is this right?

 

[ehild]

It is right. Now express V(R2) using the electric field between the innermost sphere and the middle one.

 

[Saitama]

It is right. Now express V(R2) using the electric field between the innermost sphere and the middle one.

V(R_2)-V(R_1)=-\int_{R_1}^{R_2} \frac{-kQ}{r^2} dr
Solving
V(R_2)=kq_1 \left(\frac{1}{R_1}-\frac{1}{R_2}\right)

Equating both the expressions
(Q-q_1)\left(\frac{1}{R_2}-\frac{1}{R_3}\right)=q_1 \left(\frac{1}{R_1}-\frac{1}{R_2}\right)
Solving,
q_1=\frac{Q\left(\frac{1}{R_2}-\frac{1}{R_3}\right)}{\left(\frac{1}{R_1}-\frac{1}{R_3}\right)}

Do I need to use $Q-q_1$ and the potential at the surface of the middle sphere in the equation $Q=C_{self}V$?

 

[ehild]

You have q1, and can plug that into any equation for V(R2). The charge of the middle sphere is Q. q1 and Q-q1 are the surface charges.

ehild

 

[Saitama]

You have q1, and can plug that into any equation for V(R2). The charge of the middle sphere is Q. q1 and Q-q1 are the surface charges.

ehild

C_{self}=\frac{Q}{V(R_2)}
=\frac{Q}{V(R_2)}=\frac{Q}{kq_1 \left(\frac{1}{R_1}-\frac{1}{R_2}\right)}

Should I substitute the value of $q_1$ in this expression?

 

[ehild]

Yes. It is not THAT terrible

 

[Saitama]

Yes. It is not THAT terrible

I plugged in the values and got 13.5*10^8 but this is wrong. :(

 

[ehild]

What is your formula for Cself? Have you plugged in k?

 

[Saitama]

What is your formula for Cself?

I posted it above in one of my post. :-)

Oops, I guess I realized my mistake.