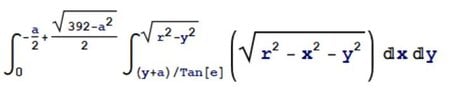Calculating Sphere Volume Cut by 2 Planes & Angle "e" & Distance "a

[zhaojx84]

I want to calculate the volume of a sphere cut by two arbitrary plane. There is a intersection angle between these two planes, which is not 90 degrees. One of these two planes is fixed and located on plane "x-o-y", and the other is perpendicular to plane "x-o-z" and moves the distance "a" from the original point.
How to establish the relationship between the volume of a sphere cut by these two arbitrary plane and the distance "a"?
I set up the double integral as follows. The "e" is the intersection angle between these two planes, and the "r" is the radius of this sphere, both of which can be assumed to be a value.
View attachment 7714

 

[jvicens]

To establish the relationship between the volume of a sphere cut by these two arbitrary planes and the distance "a", we can use a double integral to calculate the volume of the intersection region.

First, we can define the sphere as a function in spherical coordinates, with the center at the origin and the radius "r". This can be written as:
f(θ,ϕ) = r

Next, we can define the two planes as functions in Cartesian coordinates. The fixed plane on the x-o-y plane can be written as:
g(x,y) = 0

The moving plane, perpendicular to the x-o-z plane and distance "a" from the origin, can be written as:
h(x,z) = a

To find the intersection region, we can set the two plane functions equal to each other and solve for the values of x and y. This will give us the limits of integration for the double integral.

x = a
y = √(r^2 - a^2)

Now, we can set up the double integral using these limits of integration and the function of the sphere in spherical coordinates.

V = ∫∫f(θ,ϕ) dA
V = ∫∫r sin(θ) dθdϕ
V = r ∫∫sin(θ) dθdϕ

Using the limits of integration for x and y, we can rewrite the double integral in terms of θ and ϕ.

V = r ∫∫sin(θ) dθdϕ
V = r ∫0^π/2∫0^2π sin(θ) dθdϕ

Now, we can solve the double integral and substitute the value for θ.

V = r ∫0^π/2∫0^2π sin(θ) dθdϕ
V = r ∫0^2πdϕ
V = 2πr

Finally, we can substitute the value for "a" into the equation to get the final relationship between the volume of the intersection region and the distance "a".

V = 2πr(a)

In conclusion, the relationship between the volume of a sphere cut by two arbitrary planes and the distance "a" is given by the equation V = 2πr(a), where "r" is