Calculating Tension on a Plastic Ring

[dE_logics]

Imagine a ring; the image below shows the top cross section of the ring -

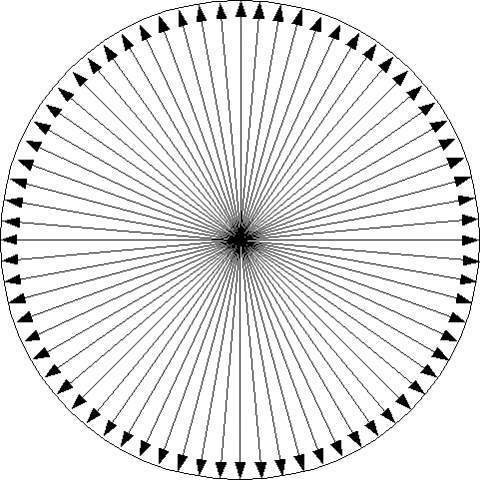
The arrows represent forces which is acting towards the inner side of the ring cause of a pressure which applies towards it's inner side.

Assuming the ring to be made up of a material having a plastic property, I want an expression for the tension produced in the ring.

 

[minger]

Do you own a copy of Roark? This looks like a ring under internal pressure. Actually, the load case you probably want is a simple shell of revolution under internal pressure. In my version its Chapter 13 load case 1b.
Hoop stress:
$$\sigma = \frac{qR}{t}$$

 

[FredGarvin]

That is pretty much the definition of the hoop stress.

 

[dE_logics]

You all mean this -

http://en.wikipedia.org/wiki/Cylinder_stresses

Right?

So this hoop stress...can this be a direct measure of the stress in the ring?

 

[dE_logics]

I did some calculations and found that the stress should be ~63.7% of 1/4th of the total force applied by the pressure.

 

[minger]

?

 

[FredGarvin]

I did some calculations and found that the stress should be ~63.7% of 1/4th of the total force applied by the pressure.

I understood 1/4th of 63.7% of that post. Care to rephrase this or tell us what you are getting at?

 

[dr dodge]

Do you own a copy of Roark?

is this a good book for the "techno savy" non engineer?

I would like to find a good formula book that was not a novel in "techno-ese" just formulas
(especially pressure and temp related)

dr

 

[CFDFEAGURU]

Roark's book is pretty good. If you are crafty enough with mathematics you can derive some of the formulas in Roark with the help of Timoshenko's book "Plates and Shells" but you better be good.

To answer your question:

Roark's book is good for the non-engineer. The hard part is knowing that you have the right boundary conditions specified.

Here is a link to it.

http://www.roarksformulas.com/

Be cautious of the online calculator.

Thanks
Matt

 

[FredGarvin]

It is but you do have to have a basic understanding to fully understand it. The beginning sections of each chapter cover theory. However, it is, essentially, a book divided into different tables covering load/support scenarios with associated equations covering that scenario. I attached a typical page so you can see it.

 

[dE_logics]

?

aaa...just forget the 63.7% part...I'll work on it later.


Point is hooks stress is no different from normal stress right?...I mean if hook's stress comes as 500 mega pascals, then the stress in the material is 500 mega pascals right?

 

[Brian_C]

The hoop stress is very easy to derive for this type of setup. There is no need for any fancy elasticity theory.

 

[nvn]

Point is, hooks [sic] stress is no different from normal stress, right? ... I mean, if hook's [sic] stress comes as 500 megapascals, then the stress in the material is 500 megapascals, right?

dE_logics: That is correct. Hoop stress is normal stress. Very good.

 

[dE_logics]

dE_logics: That is correct. Hoop stress is normal stress. Very good.

Sounds sarcastic.

Is there a conversion or something?

 

[FredGarvin]

No. He was being serious. The hoop stress is the same thing as the normal stress because of the direction on an element that is perpendicular to a line around the circumference at some radius.

 

[dE_logics]

Oh...ok, thanks a lot people.

Need it urgently.

 

[dr dodge]

thanks for the book review
I'll add it to my "wish list" when I go to the used book store
if not, it looks like it is worth the $70 anyway

dr