- #1
evinda
Gold Member
MHB
- 3,836
- 0
Hello! (Wave)
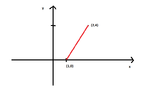
A ship that is at the position $(1,0)$ of a chart ( with the north at the positive direction $y$) "sees" a rock at the position $(2,4)$. Which is the vector that connects the ship with the rock? What angle $\theta$ does this vector form with the direction of the north?
I have thought to draw the x and y-axis:
View attachment 5319
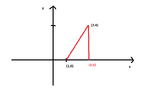
The vector that connects the ship with the rock is $(1,0)+ t (1,4), t \in \mathbb{R}$, isn't it?We consider the triangle:
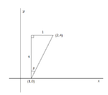
View attachment 5320Do we have to prove that it is a right triangle in order to use for example that $\sin {\phi}= \frac{\text{opposite}}{\text{hypotenuse}}$ ?
A ship that is at the position $(1,0)$ of a chart ( with the north at the positive direction $y$) "sees" a rock at the position $(2,4)$. Which is the vector that connects the ship with the rock? What angle $\theta$ does this vector form with the direction of the north?
I have thought to draw the x and y-axis:
View attachment 5319
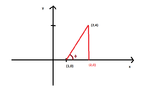
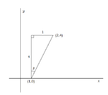
The vector that connects the ship with the rock is $(1,0)+ t (1,4), t \in \mathbb{R}$, isn't it?We consider the triangle:
View attachment 5320Do we have to prove that it is a right triangle in order to use for example that $\sin {\phi}= \frac{\text{opposite}}{\text{hypotenuse}}$ ?