Calculating the angle of the force exerted on a pulley

[riddle]

Homework Statement

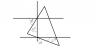
Figure 3 shows a particle X of mass 3 kg on a smooth plane inclined at an angle 30° to the
horizontal, and a particle Y of mass 2 kg on a smooth plane inclined at an angle 60° to the
horizontal. The two particles are connected by a light, inextensible string of length 2.5 metres
passing over a smooth pulley at C which is the highest point of the two planes.
Initially, Y is at a point just below C touching the pulley with the string taut. When the
particles are released from rest they travel along the lines of greatest slope, AC in the case of
X and BC in the case of Y, of their respective planes. A and B are the points where the planes
meet the horizontal ground and AB = 4 metres.

By finding the tension in the string, or otherwise, find the magnitude of the force
exerted on the pulley and the angle that this force makes with the vertical.

Homework Equations

n/a

The Attempt at a Solution

I've worked out the acceleration to be: 0.1g(2$$\sqrt{}$$3 - 3)
And the force exerted on the pulley is T$$\sqrt{}$$2, where T=3*acceleration + 3gcos60.
Where "g" is approximately 9.8m/(ss)
What I don't get is what the "angle that this force makes with the vertical" is.

 

[Doc Al]

What I don't get is what the "angle that this force makes with the vertical" is.

Did you find the tension in the string? What's the net force on the pulley exerted by the string? (What force does each side of the string exert on the pulley? Add up the force vectors.)

 

[riddle]

Yes. The tension is approximately 16.064 N. Making the net force exerted on the pulley around 22.719 N. But I still don't see how I find the angle.

 

[Doc Al]

Yes. The tension is approximately 16.064 N.

I haven't verified that, but OK.

Making the net force exerted on the pulley around 22.719 N.

How did you determine this?

What forces act on the pulley? Give their magnitude and direction.

 

[riddle]

I made a triangle, used the angles to and saw that the triangle was a right triangle, using pytahgagoras i found the magnitude of the force exerted on the pulley. I don't know how to find the direction.

 

[Doc Al]

OK.

One way to find the direction of the resultant is to use the component method. Find the vertical and horizontal components of each force vector, then add them to get the components of the resultant.

 

[riddle]

I don't understand.

Oh and this is what it says on the answer page thing:
force on pulley = 22.7 N
force acts at an angle 45° to each plane i.e. 15° to vertical

 

[Doc Al]

Oh and this is what it says on the answer page thing:
force on pulley = 22.7 N
force acts at an angle 45° to each plane i.e. 15° to vertical

That works. Draw a vector addition triangle (A + B = C). You know the angle and the length of each vector. Since the sides of the triangle are equal, you know that the angles opposite those sides must be equal. (It's an isosceles right triangle.) That will tell you the angle that the resultant makes with each force vector (which are parallel to the planes), which will tell you the angle it makes with the vertical.

Or you can just use components. Not quite as clever, but it will give you the answer just the same. What are the components of each tension force vector?

 

[riddle]

Ok, now I'm just uber confused.
At first I thought that the angles in the diagram (see thumbnail) were the angles that the tension made, but then I realized that the triangle is isosceles, so the angles would have to be the same, but that's not the case. What are the angles created by the tension then?

 

[Doc Al]

At first I thought that the angles in the diagram (see thumbnail) were the angles that the tension made,

They are. The tension is parallel to the planes, thus the tension forces make the same angle with the horizontal.

but then I realized that the triangle is isosceles, so the angles would have to be the same, but that's not the case.

The force addition triangle is isosceles. You need to draw that. (It's not the same as the apparent triangle that the wedge shaped plane makes, if that's what you're thinking.)

Draw a force diagram: Tension 1 + Tension 2 = Resultant force. The directions of those tension forces will be parallel to their respective planes.

 

[riddle]

But isn't the vector of the resultant force parallel to the horizontal?

 

[Doc Al]

But isn't the vector of the resultant force parallel to the horizontal?

No, not at all. You're confusing the bottom of the wedge with the resultant. They have nothing to do with each other.

Draw a vector represent tension #1. It will make an angle of 60 degrees with the horizontal.

Draw a vector represent tension #2. It will make an angle of 30 degrees with the horizontal.

These two vectors will have the same length.

Now draw their sum. (Do you know how to add vectors graphically? See: http://hyperphysics.phy-astr.gsu.edu/hbase/vect.html#vec1")

 

[riddle]

Ah, I understand. But, I still don't see how you work out the angles. Can you please draw it for me? I would really appreciate it.

 

[Doc Al]

Ah, I understand. But, I still don't see how you work out the angles. Can you please draw it for me? I would really appreciate it.

You give it a try. Let the first vector be an arrow (length = T) going downward to the left, making an angle of 30 degrees below horizontal (and 60 degrees to the left of vertical).

Starting at the point of that first vector, draw the tail of second vector. It will be an arrow (length = T) going downward to the right, making an angle of 60 degrees below horizontal (and 30 degrees to the right of vertical).

Complete the triangle.

 

[riddle]

Why do I have a feeling that this (thumbnail) isn't right.

And if it is right. I don't see how it helps.
*sigh*

 

[Doc Al]

Why do I have a feeling that this (thumbnail) isn't right.

And if it is right. I don't see how it helps.
*sigh*

Well, it's kind of right. (Your angles seem to be marked correctly, but they aren't too close to scale. What you call 60 degrees looks more like 30 and vice versa. And I don't see arrows, just lines. But ok. )

In any case, you have the two equal sides of your isosceles right triangle. So what must the angles opposite those sides equal?

 

[riddle]

lol, I've never been good with to-scale diagrams.
meh. I don't see any of the angles inside the triangle. All I know is that the two angles opposite the one in the "center" are equal, meaning the "center" angle is 180 - twice one of the angles.
(I can't wait till all this seems like kid's stuff)

 

[Doc Al]

You agree, I hope, that there are three angles in the triangle. What do they add to? One of them is 90 degrees (it's a right triangle). Since the other two are equal, what must they be?

 

[riddle]

OH! It's a right triangle. I thought I saw that, but then I remembered you telling me that the triangle in the drawing was different from the force triangle. And it is different. But! It's still a right triangle.
But one question. How do you draw the triangle you told me to draw. With the angles I mean. Where do you get those angles from? Well stupid question. Their from the original diagram. But how do you know what to do with them?
Meh. I should take a nap. I feel stupid.