- #1
Nemo1
- 62
- 0
Hi Community,
I have this question and I stuck on the last question:
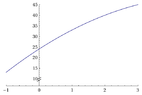
(b) How many subintervals do you need to estimate the area to within 0.1units\(\displaystyle ^2\)
View attachment 5069
I thought it was 40 subintervals but I am thinking that my answer is divisions along the $x$ axis.
The other questions I am confident I have been able to answer.
Any help would be appreciated.
Cheers Nemo.
I have this question and I stuck on the last question:
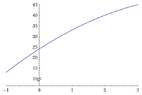
(b) How many subintervals do you need to estimate the area to within 0.1units\(\displaystyle ^2\)
View attachment 5069
I thought it was 40 subintervals but I am thinking that my answer is divisions along the $x$ axis.
The other questions I am confident I have been able to answer.
Any help would be appreciated.
Cheers Nemo.
Attachments
Last edited: