- #1
phospho
- 251
- 0
Could anyone tell me how they found the area of the triangle?
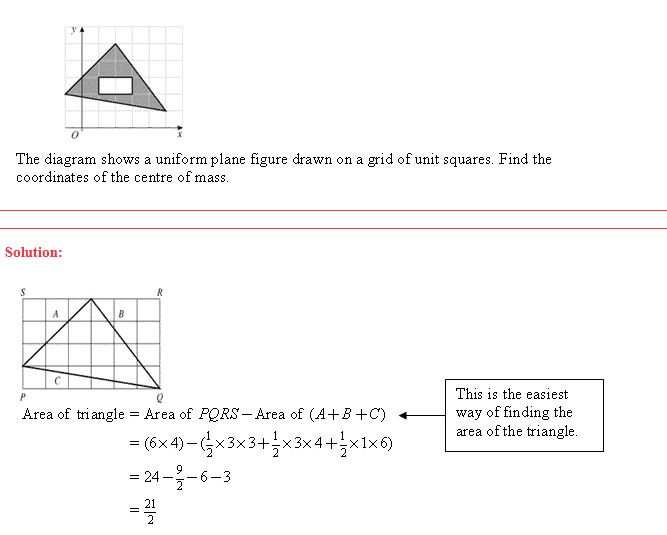
When I try to use 0.5*b*h I get 10.64483443, not 10.5
When I try to use 0.5*b*h I get 10.64483443, not 10.5