Calculating the energy in an EM wave

[fisher garry]

You don't have to read all this theory to answer my question. I added it just in case.

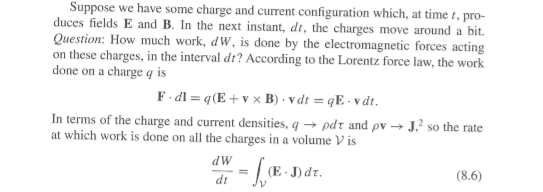
Above they use the definition work energy theorem in vacuum to get to (8.12). Since it is in vacuum I would guess that one could use the equations for B and E field from EM-waves so that magnitude poynting vector due to orthogonality of B and E field of EM-waves this becomes:

$|\frac{1}{\mu_0} \pmb{E}\times \pmb{B} |=\frac{1}{\mu_0} \pmb{E} \pmb{B}$

by using
$\pmb{E}=c \pmb{B}$

$|\frac{1}{\mu_0} \pmb{E}\times \pmb{B} |=\frac{1}{\mu_0} c \pmb{B^2}$

Is it possible to expand this so that you can calculate the energy of a single EM-wave? By integrating (8.12) or something? It should be equal to E=hf if I am not wrong.

 

[ZapperZ]

What exactly is ".. a single EM-wave..."? And why should this be equal to hf? hf is the energy of a single photon. This is not a "... single EM-wave...".

Zz.

 

[fisher garry]

What exactly is ".. a single EM-wave..."? And why should this be equal to hf? hf is the energy of a single photon. This is not a "... single EM-wave...".

Zz.

Is there a mathematical relation between energy in a photon and energy of an EM-wave?

 

[Vanadium 50]

If you ignore people's requests for clarification ('What exactly is ".. a single EM-wave..."? ') you will not get the most useful replies and you will not be getting the most out of PF.

 

[Nugatory]

Is there a mathematical relation between energy in a photon and energy of an EM-wave?

No. There is a mathematical relationship between the energy and the frequency of a photon, but the relationship between photons and electromagnetic waves is much more complicated and nothing like what you imagine when you hear things like “light is made of particles called photons”.

Electromagnetic waves are a classical phenomenon described by classical electrodynamics. Photons don’t come into the picture unless you’re considering quantum mechanical effects, and there aren’t any in this problem

 

[fisher garry]

No. There is a mathematical relationship between the energy and the frequency of a photon, but the relationship between photons and electromagnetic waves is much more complicated and nothing like what you imagine when you hear things like “light is made of particles called photons”.

Electromagnetic waves are a classical phenomenon described by classical electrodynamics. Photons don’t come into the picture unless you’re considering quantum mechanical effects, and there aren’t any in this problem

Do you know about a book that introduces this theory?

 

[ZapperZ]

Do you know about a book that introduces this theory?

Back up a bit. There is something very puzzling here, and it is all due to the absence of context.

You quoted a section of Griffith's E&M text, which is a common textbook for E&M courses at the undergraduate level. Typically, someone who is using this text would have gone through a complete sequence of General Physics (with calc) courses. Such a course would have included a rudimentary introduction to quantum physics and the concept of photons.

But yet, here you are, asking for "... a book that introduces this theory..."? As in quantum physics?

I do not understand this. How are you able to jump to Griffith's text, and yet, not have an idea of the basic idea of photons that is typically introduced at the General Physics level? And if you want something more advanced, Griffith also has an undergraduate text in Quantum Mechanics.

So, were you deprived of a proper introduction to the subject of physics in your General Physics courses, or did ever take such a course?

Zz.

 

[fisher garry]

Back up a bit. There is something very puzzling here, and it is all due to the absence of context.

You quoted a section of Griffith's E&M text, which is a common textbook for E&M courses at the undergraduate level. Typically, someone who is using this text would have gone through a complete sequence of General Physics (with calc) courses. Such a course would have included a rudimentary introduction to quantum physics and the concept of photons.

But yet, here you are, asking for "... a book that introduces this theory..."? As in quantum physics?

I do not understand this. How are you able to jump to Griffith's text, and yet, not have an idea of the basic idea of photons that is typically introduced at the General Physics level? And if you want something more advanced, Griffith also has an undergraduate text in Quantum Mechanics.

So, were you deprived of a proper introduction to the subject of physics in your General Physics courses, or did ever take such a course?

Zz.

I have a degree in chemistry where i had physical chemistry 1 and 2 and 2 physics courses. I am drawn towards physics and is therefore reading it by myself. One of the two physics courses was introduction course in electromagnetism. I would imagine that griffiths intro to electromagnetism is a bit more advanced so i could read that. What kind of textbook introduces photons theory? One of my phys chem courses was int course to quantum mech so i don't know if i would be able to read quantum theory about photons.

 

[ZapperZ]

I have a degree in chemistry where i had physical chemistry 1 and 2 and 2 physics courses. I am drawn towards physics and is therefore reading it by myself. One of the two physics courses was introduction course in electromagnetism. I would imagine that griffiths intro to electromagnetism is a bit more advanced so i could read that. What kind of textbook introduces photons theory? One of my phys chem courses was int course to quantum mech so i don't know if i would be able to read quantum theory about photons.

Once again, as someone who is teaching General Physics courses for both calc-based and non-calc based, how come you did not encounter Modern Physics in your General Physics courses? Was such a topic not included? What text did you use? If that topic was not covered, chances are it is still included in the text. Start there!

Zz.

 

[fisher garry]

Once again, as someone who is teaching General Physics courses for both calc-based and non-calc based, how come you did not encounter Modern Physics in your General Physics courses? Was such a topic not included? What text did you use? If that topic was not covered, chances are it is still included in the text. Start there!

Zz.

The other physics course I had was an introductionary general physics course so i guess what it would say about photons would be non mathematical in the context i was looking for. I guess a better textbook could help

 

[Nugatory]

Do you know about a book that introduces this theory?

That would be a quantum electrodynamics text. Be aware, however, that quantum electrodynamics is generally considered a graduate-level topic for students who have completed a BA in physics and are on their way to a PhD.

 

[vanhees71]

I think it is very important to get some order in thinking about this problem before you start. First of all you deal with classical electrodynamics. If you read the word "classical" then it's utmost always clear that nowhere Planck's constant $h=2 \pi \hbar$ can occur, because this quantity is introduced into physics only within quantum theory. So don't confuse yourself with thinking about electromagnetic problems, which deal with classical electromagnetism, in terms of "photons" or other quantum concepts. Photons are anyway closer to classical wave theory than classical mechanics, i.e., the most simple picture of electromagnetic phenomena is the field picture anyway. If you have to deal with quantum theory of electromagnetic phenomena, i.e., quantum electrodynamics, you have to study quantum electrodynamics (QED), which is more advanced than classical electrodynamics, and you need a very good understanding of classical electrodynamics first, before starting studying QED.

Now you deal with general fields within classical electrodynamics, not special solutions thereof. So you cannot assume that $\vec{E}$ and $\vec{B}$ are perpendicular to each other. In the context of waves this is only the case for plane-wave modes, which are only solutions of Maxwell's equations in source-free regions (i.e., in regions without currents and charges).

What's supposed to be calculated is the energy balance of electromagnetic fields interacting with charges and currents in general, starting from the energy distribution and flow of the electromagnetic field. Physically it's clear what must come out: If there were no charge-current distributions around the total energy of the electromagnetic field would be conserved, and in local form this means the energy density of the em. field
$$u_{\text{em}}=\frac{\epsilon_0}{2} \vec{E}^2 + \frac{1}{2 \mu_0} \vec{B}^2$$
and the energy-current density
$$\vec{S}_{\text{em}}=\frac{1}{\mu_0} \vec{E} \times \vec{B}$$
would obey the continuity equation, expressing the fact that the only way energy can changing within a volume if energy is transported through its boundary surface, i.e.,
$$\partial_t u_{\text{em}} + \vec{\nabla} \cdot \vec{S}_{\text{em}}=0 \quad \text{for} \quad \rho=0, \quad \vec{j}=0.$$
If however charges and currents are present the field also interacts with them and the charges get accelerated through this interaction. Thus you must get something on the right-hand side of the continuity equation, i.e., the energy per unit time transferred to the charges. Since the force per unit volume is $$\vec{f}=\rho (\vec{E} + \vec{v} \times \vec{B})$$, the power per unit volume transferred to the charges is $$\vec{v} \cdot \vec{f}=\rho \vec{v} \cdot \vec{E}=\vec{j} \cdot \vec{E}$$. From the point of view of the em. field this is "lost energy per time and volume", i.e., you must get
$$\partial_t u_{\text{em}} + \vec{\nabla} \cdot \vec{S}_{\text{em}}=-\vec{j} \cdot \vec{E}.$$
This is "Poynting's theorem", and you can prove it with help of the Maxwell equations. This is what Griffiths demonstrates in #1.

The time derivative of the em. energy density is straight-forward to calculate. You only need
$$\partial_t (\vec{E}^2)=2 \vec{E} \cdot \partial_t \vec{E}, \quad \partial_t (\vec{B}^2)=2 \vec{E} \cdot \partial_t\vec{B}.$$

The calculation of $\vec{\nabla} \cdot \vec{S}$ is easier in the Ricci calculus, where you deal with the components and with partial derivatives rather than with the vector notation and nabla calculus:
$$\mu_0 \vec{S}=\vec{E} \times \vec{B}\; \Rightarrow \; \mu_0 S_j =\epsilon_{jkl} E_k B_l.$$
Here we imply Einstein's summation convention over repeated indices, and $\epsilon_{jkl}$ is the totally antisymmetric Levi-Civita symbol with $\epsilon_{123}=1$. Now
$$\mu_0 \vec{\nabla} \cdot \vec{S}_{\text{em}}=\partial_j (\epsilon_{jkl} E_k B_l)=\epsilon_{jkl} (B_l \partial_j E_k + E_k \partial_j B_l)=\vec{B} \cdot (\vec{\nabla} \times \vec{E})-\vec{E} \cdot (\vec{\nabla} \times \vec{B}).$$
This leads to
$$\partial_t u_{\text{em}}+\vec{\nabla} \cdot \vec{S}_{\text{em}} = \epsilon_0 \vec{E} \cdot \partial_t \vec{E} + \frac{1}{\mu_0} \vec{B} \cdot \partial_t \vec{B} +\frac{1}{\mu_0} [ \vec{B} \cdot (\vec{\nabla} \times \vec{E})-\vec{E} \cdot (\vec{\nabla} \times \vec{B})].$$
Faraday's Law,
$$\vec{\nabla} \times \vec{E}=-\partial_t \vec{B}$$
cancels the 2nd against the 3rd term:
$$\partial_t u_{\text{em}}+\vec{\nabla} \cdot \vec{S}_{\text{em}} =\epsilon_0 \vec{E} \cdot \partial_t \vec{E} - \frac{1}{\mu_0} \vec{E} \cdot (\vec{\nabla} \times \vec{B}).$$
However, the Maxwell-Ampere Law tells you that
$$\frac{1}{\mu_0} \vec{\nabla} \times \vec{B}= \vec{j} + \epsilon_0 \partial_t \vec{E}$$.
Plugging this into the previous equation finally gives
$$\partial_t u_{\text{em}}+\vec{\nabla} \cdot \vec{S}_{\text{em}} =-\vec{j} \cdot \vec{E},$$
which is what we wanted to prove.

 

[fisher garry]

You might be tired of my reasoning but

The theory above made me wonder

One set of possible solutions to maxwell are

It is known that deacceleration of an electron creates EM-waves. If you have a constant acceleration of an electron from a B field and stops the electron then all kinetic energy should be given out as an EM-wave so that

Anyone have anything to add of an experiment that could determine the frequency of an EM-wave this way?

 

[Nugatory]

It is known that deacceleration of an electron creates EM-waves

yes, but...

If you have a constant acceleration of an electron from a B field and stops the electron then all kinetic energy should be given out as an EM-wave

No, because a magnetic field cannot stop an electron - the force it prduces is always perpendicular to the direction of motion so does not change its kinetic energy. You can google for "synchrotron radiation" to see what does happen.

You could in principle use an E field to slow and stop an electron, but radiation produced by this interaction is not going to be a coherent plane wave for which "the frequency" is defined. Google for "bremsstrahlung" to see what really happens when a fast-moving electron is stopped.

 

[vanhees71]

Of course an electron moving in a magnetic field is accelerated and thus looses kinetic energy through radiation of em. waves. That's synchrotron radiation and particularly for electrons a nuissance for particle physicists who want to accelerate the electrons to high speeds. That's why usually you have to use linear accelerators for electrons.

It's clear that the general calculation in #12 is valid also in this case. The energy loss is not directly through the external magnetic field but due to the electric field due to the charge of the electron itself. Note that the "radiation-reaction problem" is not fully solvable for classical point particles!

 

[fisher garry]

In the theory above they derive a perturbation wave. They refer to it as an eletromagnetic wave in the end but they don't give it a sinusoidal oscillation. Does this perturbation wave have a frequency or does it not?

 

[sophiecentaur]

Does this perturbation wave have a frequency or does it not?

I think you are rather desperate to show yourself 'not wrong' here, by quoting random bits of theory.

"This perturbation", along with many other perturbations, doesn't have to have a "frequency". The term 'frequency" implies an infinite train of identical repeating waveforms. Just go "Tick" to produce your own wave that lasts for a very short time and which consists of a large number of waves with frequencies that are identifiable only for a short time.

There is a lot of superficial treatment of waves and photons which lead to confusion. I can safely say that none of us, on PF, have a perfect knowledge of all this stuff. We just use it at a depth we can get on with. The Poster Boy of Physics, Richard Feynman is quoted to have said that anyone who claims to understand Quantum Mechanics doesn't. So be prepared to encounter many apparent paradoxes in your journey in this direction.

 

[fisher garry]

Ok I know you are tired of my adressings. But one is coming up unfortunately.

This is going to be a bit of a long thread. I will start with the kinetic energy relation from a revolving current coil that finds it equilibrium and stop after turning 90 degrees:

So above we have two formulas for the kinetic energy of a revolving of 90 degrees of a circular current

Now an adressing of the pressure of an EM wave taken from Tipler and Mosca general physics book:

And then a calculation of the frequency of a hypothetical photon (that is if all energy is transferred to a photon)

How come I don't get the same value for the frequencies?

 

[ZapperZ]

Question: what makes you think that the loop turns due to "radiation pressure"? Isn't this something that you need to justify FIRST? You seem to be using it as if a valid relationship has already been established.

Zz.

 

[fisher garry]

Question: what makes you think that the loop turns due to "radiation pressure"? Isn't this something that you need to justify FIRST? You seem to be using it as if a valid relationship has already been established.

Zz.

There is an external magnetic field which I denote as $B_{ext}$ in the final part which will turn the current coil 90 degrees until it reaches equilibrium in the first part. In the first part I call this $B_{ext}$ only for B (it is in the final part that we have two B fields). From the drawing you will see that at equilibrium the forces drags it out at both sides but that it will not move. This is a normal setup in introductionary courses of electromagnetism so I am not sure where radiation pressure comes in here? It is introduced in the next part and then I say that I want all the kinetic energy from the revolving coil to bemoved to a hypothetical photon.

 

[ZapperZ]

There is an external magnetic field which I denote as $B_{ext}$ in the final part which will turn the current coil 90 degrees until it reaches equilibrium in the first part. In the first part I call this $B_{ext}$ only for B (it is in the final part that we have two B fields). From the drawing you will see that at equilibrium the forces drags it out at both sides but that it will not move. This is a normal setup in introductionary courses of electromagnetism so I am not sure where radiation pressure comes in here? It is introduced in thr nrxt part and then I say that I want all the kinetic energy from revolving the coil moved to a hypothetical photon.

But why would this have anything to do with "radiation pressure"? You didn't answer my previous question with that "explanation".

Zz.

 

[fisher garry]

But why would this have anything to do with "radiation pressure"? You didn't answer my previous question with that "explanation".

Zz.

This is a normal setup in introductionary courses of electromagnetism so I am not sure where radiation pressure comes in here? It is introduced in the next part and then I say that I want all the kinetic energy from the revolving coil to bemoved to a hypothetical photon.

Agree or disagree? That I guess would be the question?

 

[ZapperZ]

This is a normal setup in introductionary courses of electromagnetism so I am not sure where radiation pressure comes in here? It is introduced in the next part and then I say that I want all the kinetic energy from the revolving coil to bemoved to a hypothetical photon.

Agree or disagree? That I guess would be the question?

But that exactly is what I'm asking. Why should there be a connection between such radiation pressure/hypothetical photon to your coil dynamics? You have two separate situations, and yet, you are connecting them together as if the connection is clear and obvious. This has NOT been established!

I know all about the interaction of a loop of current with an external static magnetic field. I teach that topic! So stop telling me that it is a "normal setup in introductory course". That isn't the issue!

Zz.

 

[fisher garry]

But that exactly is what I'm asking. Why should there be a connection between such radiation pressure/hypothetical photon to your coil dynamics? You have two separate situations, and yet, you are connecting them together as if the connection is clear and obvious. This has NOT been established!

I know all about the interaction of a loop of current with an external static magnetic field. I teach that topic! So stop telling me that it is a "normal setup in introductory course". That isn't the issue!

Zz.

I understand what you meant now:) That was one of the things I wondered about. In Tipler and Mosca they use the following equation.

I Will add some more of the theory just in case there are any relations. This is the theory that I used for the white middle part above:

The poynting vector is per area and time unit and I have not introduced anything about area I guess.

 

[ZapperZ]

Why in the world are we dealing with radiation pressure in the first place? Why do you think it has any relevance in describing Faraday's law? Why haven't you answered that?

Zz.

 

[fisher garry]

Why in the world are we dealing with radiation pressure in the first place? Why do you think it has any relevance in describing Faraday's law? Why haven't you answered that?

Zz.

I think I understand. Let me change the scenario. You have a circular current coil and apply an external B field. I will rewrite the relations of the kinetic energy produced:

When the coil has turned 90 degrees it reaches equilibrium and deaccelerates to 0 velocity. Let's assume hypotetically that all this energy is released as one photon. Now I will try to introduce radiation pressure again:

So we hypotetically want the electron that has been deaccelerated to 0 velocity (I will ignore the current direction) to obtain the same kinetic energy and velocity. We want it to absorb a photon to do so. If we look at one half cycle of an EM wave that would be half of the energy of one photon if all of the energy of the photon is contained in one cycle. The EM wave exert radiation pressure as described above. It is also said that E=pc where p is radiation pressure density and E is energy density.

Over a half cycle of an EM wave the avearge cycle can be obtained the following way:

In order to calculate the amplitude of the EM wave I try the following:
First I calculate the kinetic energy from the 90 degrees turn of the circular coil

Then I try to find the amplitude of the EM wave and uses the theory for the radiation pressure above along with E=pc:

Is this also a wrong usage of the radiation pressure?

 

[ZapperZ]

When the coil has turned 90 degrees it reaches equilibrium and deaccelerates to 0 velocity. Let's assume hypotetically thst all this energy is released as one photon.

LET'S NOT!

This is silly. There is nothing here that indicates that this is valid. Do you think an electron oscillating up and down and just performed half a cycle produces ONE photon? Says who? What physics are you using to justify this?

You are making all of this up.

Zz.

 

[fisher garry]

LET'S NOT!

This is silly. There is nothing here that indicates that this is valid. Do you think an electron oscillating up and down and just performed half a cycle produces ONE photon? Says who? What physics are you using to justify this?

You are making all of this up.

Zz.

Ok. Thanks for the answer. Yes most of this is something I have made myself so a reference is of course not available. I did assume that half of the energy of one photon was absorbed from a half cycle. Perhaps that is wrong. I also wondered when I used the theory of the radiation pressure from Tipler and Mosca why a higher velocity of the electron that the EM wave excerted radiation pressure on would lead to higher radiation pressure.

 

[davenn]

Ok. Thanks for the answer. Yes most of this is something I have made myself so a reference is of course not available.

Did you forget about the bit in the forum rules that comments about no personal theories ?
best you have a reread before commenting further

Speculative or Personal Theories:

Physics Forums is not intended as an alternative to the usual professional venues for discussion and review of new ideas, e.g. personal contacts, conferences, and peer review before publication. If you have a new theory or idea, this is not the place to look for feedback on it or help in developing it.

For further explanation of our policy on personal theories and speculative posts, and the history behind it, see the following entry in the Physics Forums FAQ:

https://www.physicsforums.com/threads/physics-forums-faq-and-howto.617567/#post-4664231

 

[weirdoguy]

Perhaps that is wrong

Just stop thinking and talking about photons. You are learning classical electrodynamics, not quantum.

 

[fisher garry]

I have been working a bit more and this time I ended up with some relations that could have the right numbers. So hopefully it is ok that I post this as I am not sure where else I would post.

in the theory in the top of this post there is also a volume integral which starts the derivation below:

The volume needed to make this calculation work seems to be very close to the volume of the 1s of the hydrogen atom. It also seems to denote V=constant for an energy outlet of an electron since the classical electron radius is denoted as the radius where electrons emits photons. Can anyone explain why this is wrong or not?

 

[ZapperZ]

The volume needed to make this calculation work seems to be very close to the volume of the 1s of the hydrogen atom.

How can you tell? Your work was completely devoid of units! A omission like this in my intro class will incur points deduction.

And what is the "volume" of the 1s hydrogen that you are using? And why should this be of significance other than a broad coincidence (assuming that your calculation is valid and correct, which is a big assumption)?

It is still a puzzle what exactly you are obsessing... er... calculating for.

Zz.

 

[Vanadium 50]

Seriously, learn to use TeX. Posting microscopic pictures is disrespectful of the time and effort people have put in trying to help you. Use units, like Zz said. Making people guess is disrespectful of the time and effort people have put in trying to help you. Finally, explainnwhat the heck you are trying to do rather than just dumping a big-wall-O-calculations. Doing otherwise is disrespectful of the time and effort people have put in trying to help you.

 

[fisher garry]

I guess I could write it down in tex

$\textbf{F}\cdot d \textbf{l}=q (\textbf{E} +\textbf{v}\times\textbf{B})\cdot \textbf{v}dt=q \textbf{E} \cdot \textbf{v}dt$

current density is defined as $\textbf{J}=\rho \textbf{v}$

$\textbf{F}\cdot d \textbf{l}=\frac{q}{\rho} \textbf{E} \cdot \textbf{J}dt$

Maxwell-Ampere's law:

$\textbf{E} \cdot \textbf{J}=\frac{1}{\mu _0}\textbf{E} \cdot (\nabla \times \textbf{B})- \epsilon _0 \textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t}$

the identity

$\nabla \cdot (\textbf{E} \times \textbf{B})= \textbf{B} (\nabla \times \textbf{E}) - \textbf{E} \cdot (\nabla \times \textbf{B})$

We also have
$\textbf{B} \cdot \frac{\partial \textbf{B}}{\partial t}= \frac{1}{2} \frac{\partial }{\partial t} B^2$

$\textbf{E} \cdot \frac{\partial \textbf{E}}{\partial t}= \frac{1}{2} \frac{\partial }{\partial t} E^2$

$\textbf{E} \cdot \textbf{J}= \frac{1}{2} \frac{\partial }{\partial t}(\epsilon _0 E^2+\frac{1}{\mu _0} B^2)-\frac{1}{\mu _0} \nabla \cdot (\textbf{E} \times \textbf{B})$

The first term to the right in the last equation is the energy density. We want to look at the energy transported out which is the second term. Since we want what goes out we change the sign

$\textbf{F}\cdot d \textbf{l}=\frac{q}{\rho} \textbf{E} \cdot \textbf{J}dt=\frac{q}{\rho} \frac{1}{\mu _0} \nabla \cdot (\textbf{E} \times \textbf{B})dt=\frac{q}{\rho} \frac{1}{\mu _0} \nabla \cdot cB^2dt$

I omitted the direction vector above because I am only looking for a quantification of the energy. Above we still have the units Joule.

Then we look at an EM-wave

$B=\textbf{B}_{0}sin[2\pi ft]=\textbf{B}_{0}sin[2\pi f\frac{x}{c}]$

$\nabla \cdot (B^2)=\textbf{B}_{0} 4 \pi f \frac{1}{c} cos[2\pi f\frac{x}{c}]$

$\frac{q}{\rho} \frac{1}{\mu _0} \nabla \cdot cB^2=\frac{q}{\rho} \frac{1}{\mu _0} \textbf{B}_{0} 4 \pi f \frac{c}{c} cos[2\pi f\frac{x}{c}]=\frac{q}{\rho} \frac{1}{\mu _0} \textbf{B}_{0} 4 \pi f cos[2\pi ft]$

We integrate over a quarter of a cycle since cos is positive in the first quarter and multiply by 4 afterwards

$4\int_{0}^\frac{T}{4}cos[2\pi ft]dt=4\frac{1}{2\pi f}(sin[2\pi f\frac{T}{4}]-sin[2\pi f 0])=2\frac{1}{\pi f}$

$E=\frac{q}{\rho} \frac{1}{\mu _0} \textbf{B}_{0} 4 \pi f 2\frac{1}{\pi f}=8 \frac{V}{\mu _0} \textbf{B}_{0}$

We still have units joule above

If all the energy was sent out from an electrons perspective instead

$\frac{dW}{dt}=\textbf{E} \cdot \textbf{J} d \tau$

By using the rewriting above and again assume that all the energy is sent out and therefore the energy density is 0:

$\frac{dW}{dt}=\frac{1}{\mu _0} \int c \cdot B^2 d \tau$

divergence theorem:

$\frac{dW}{dt}=\frac{c}{\mu _0} \int \nabla B^2 d A=\frac{c}{\mu _0}B^2 4 \pi r^2$

Again we want all the energy to be preserved in one wave

$W=4 \pi r^2\frac{c}{\mu _0} B_{0}^2 \int_{0}^T sin^2[2\pi ft] dt$

$sin^2[2\pi ft] =\frac{1}{2}- cos[4\pi ft]$

$W=4 \pi r^2\frac{c}{\mu _0} B_{0}^2 \int_{0}^T \frac{1}{2}- cos[4\pi ft] dt$

the lower limit leads to 0 since the integral of cos is sin and we are left with

$W=4 \pi r^2\frac{c}{\mu _0} B_{0}^2 ( \frac{T}{2}- sin[4\pi fT])= 2\pi r^2\frac{c}{\mu _0} B_{0}^2\frac{1}{f}$

The units are still joule

By equating the two energy relations

$W=8 \frac{V}{\mu _0} \textbf{B}_{0}=2 \pi r^2\frac{c}{\mu _0} B_{0}^2\frac{1}{f}$

$4 V= \pi r^2c \textbf{B}_{0}\frac{1}{f}$

$f= \pi r^2c \textbf{B}_{0}\frac{1}{4 V}$

If we assume that we have the ionization energy of hydrogen electron

$E_{ion}=2.1 \cdot 10^{-18}$

We try to detrmine the correpsonding magnetic field of the ionization energy:

$8 \frac{V}{\mu _0} \textbf{B}_{0}=2.1 \cdot 10^{-18}$

But we have two unknowns the volume and the B field. If we instead start with E=hf and see if we can get something that makes sense

$8 \frac{V}{\mu _0} \textbf{B}_{0}=hf$

$8 \frac{V}{h\mu _0} \textbf{B}_{0}=f$

$f4 \frac{V}{c\pi r^2}= \textbf{B}_{0}$

$E=hf=8 \frac{V}{\mu _0} \textbf{B}_{0}=8 \frac{V}{\mu _0} f4 \frac{V}{c\pi r^2}$

It is said that electrons emit photons around the classical electron radius

$r_{classical}=2.82 \times 10^{-15}$

$h=8 \frac{V}{\mu _0} 4 \frac{V}{c\pi r^2}=6.6 \times 10^{-34}$

$V^2=\frac{\mu _0}{32}c\pi r^2 6.6 \times 10^{-34}=\frac{1.26 \times 10^{-6}}{32}3 \times 10^8 \pi (2.82 \times 10^{-15})^2 6.6 \times 10^{-34}$

$V^2=19.5 \times 10^{-62}$

$V=4.419.5 \times 10^{-31}$

This volume seems to be close to the 1s volume.

In general

$h=2.7 \times 10^{-2} \frac{V^2}{r^2}=6.6 \times 10^{-34}$

The second energy relation obtained above:

$2 \pi r^2\frac{c}{\mu _0} B_{0}^2\frac{1}{f}=E$

$r^2B_{0}^2 =\frac{f\mu _0}{c2 \pi}E=\frac{E}{2.7 \times 10^{-2} \frac{V^2}{r^2}}\frac{\mu _0}{c2 \pi}E$

$V^2B_{0}^2 =\frac{E}{2.7 \times 10^{-2} }\frac{\mu _0}{c2 \pi}E=0.0255 \times 10^{-12}E^2$

$VB_{0} =1.59 \times 10^{-5}E$

and the first energy relation obtained above:

$8 \frac{V}{\mu _0} \textbf{B}_{0}=E$

$V \textbf{B}_{0} =\frac{\mu _0}{8}E=1.58 \times 10^{-5}E$

 

[Vanadium 50]

It is said that electrons emit photons around the classical electron radius

What? By whom?