Calculating the flux of a vector field

[Slimy0233]

Homework Statement

Q.18. The flux of the vector field $\vec{F}=(x+y) \hat{i}+(x-3 y) \hat{j}+x y \hat{k}$ through the surface defined by the equation $x^{2}+y^{2} \leq a^{2}, x>0, y>0$, will be
(a) $a^{4} / 8$
(b) $a^{4} / 4$
(c) $a^{2} / 8$
(d) $a^{2} / 4$

Relevant Equations

$\vec{F}=(x+y) \hat{i}+(x-3 y) \hat{j}+x y \hat{k}$

I am not sure why latex is not rendering, but here is the question.

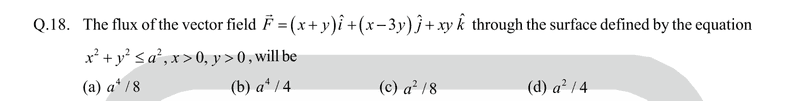
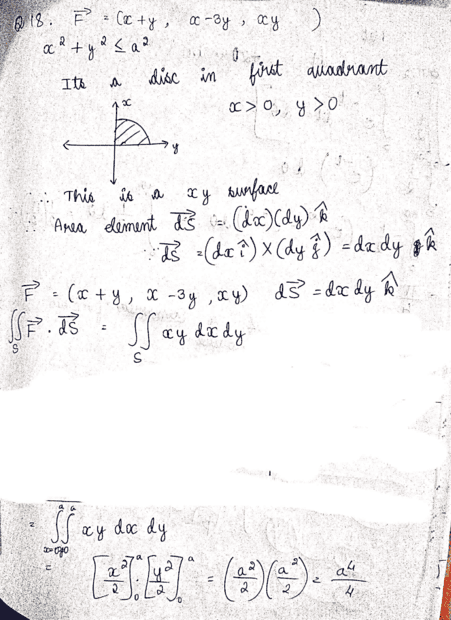
The answer is $\frac{a^2}{8}$ and for the love of my life, I don't know how. Can you please help me with this?

 

[anuttarasammyak]

\int_S xy dS= \int_0^a r^2 rdr \int_0^\frac{\pi}{2} \sin\theta \cos \theta d\theta
Azimuthal integration gives 1/2.

 

[Slimy0233]

\int_S xy dS= \int_0^a r^2 rdr \int_0^\frac{\pi}{2} \sin\theta \cos \theta d\theta
Azimuthal integration gives 1/2.

I am DOUBT! azimuthal integration is a new phrase for me. I think it's the equivalent of what I learnt as integration using spherical co-ordinates, but still, I don't see how you can get 1/2 there. Also, isn't dr 0? We are integrating with radius r as constant (a). We are given a surface x^2 + y^2 \leq a^2

 

[Steve4Physics]

I think$$\int_{x=0}^a \int_{y=0}^a xy ~dx~dy$$should actually be$$\int_{x=0}^a \int_{y=0}^{\sqrt {a^2-x^2}} xy~ dy~dx$$
And on 'dimensional' grounds, I think the answer should be a multiple of $a^4$ rather than $a^2$. So the 'official answer' might be wrong.

 

[Slimy0233]

I think$$\int_{x=0}^a \int_{y=0}^a xy ~dx~dy$$should actually be$$\int_{x=0}^a \int_{y=0}^{\sqrt {a^2-x^2}} xy~ dy~dx$$
And on 'dimensional' grounds, I think the answer should be a multiple of $a^4$ rather than $a^2$. So the 'official answer' might be wrong.

can you please explain the limits of the integral more? I mean, I put a as the limit of the integral as it's a part of a circle we are talking about here, why are you putting a different limit?

edit: Damn! Yes! It's a circle we are talking about, I seem to have calculated the area of a square. Yes?

 

[Steve4Physics]

edit: Damn! Yes! It's a circle we are talking about, I seem to have calculated the area of a square. Yes?

Yes!

 

[Steve4Physics]

can you please explain the limits of the integral more? I mean, I put a as the limit of the integral as it's a part of a circle we are talking about here, why are you putting a different limit?

Draw $xy$ axes and the 1st quadrant.

Draw a thin vertical ‘elementary’ strip of thickness $dx$ for some value of $x$ inside the quadrant. Note:
- the left side of the strip has x-coordinate $x$;
- the right side of the strip has x-coordinate $x+dx$;
- the bottom edge of the strip is a has y-coordinate = 0;
- the top edge of the strip has y-coordinate $\sqrt {a^2-x^2}$ (that’s the key point).

When you integrate $xy$ over the elementary strip you get $\int_{y=0}^{y=\sqrt {a^2-x^2}} xy~ dy~dx$. (Then it remains to integrate the contributions from all the strips.)

Can you take t from there?

 

[Slimy0233]

Can you take t from there?

It was very kind of you to explain that well and that much!

I can take it from there, thank you! I managed to solve it.