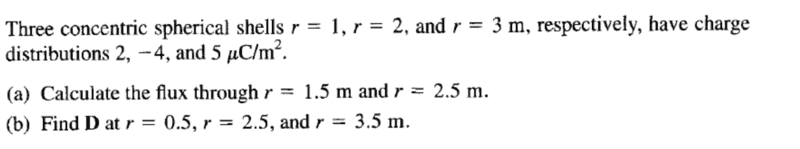BvU said:
BvU said:
In post #3 the volume integral you wrote in post #1 is replaced by a surface integral. Good ! And you write $$\phi = \oint \overline D\, \overline{dS} = Q_{enc} =\int \rho_s ds$$ where I must suppose ##D = \varepsilon_0 E## ?falyusuf said:
) but then you take ##R= 1 ## m (given) ?I was so confused in using many r's, so I use different symbols, and tried to solve it again. Here's my attempt with my explanation:BvU said:Sparse with words we are, eh ?
So what is flux in your context ? Units ?
You are asked to calculate the flux through ##r = 1.5## m as a starter in part (a).
In post #3 the volume integral you wrote in post #1 is replaced by a surface integral. Good ! And you write $$\phi = \oint \overline D\, \overline{dS} = Q_{enc} =\int \rho_s ds$$ where I must suppose ##D = \varepsilon_0 E## ?
In my book the electric flux in such a nice spherically symmetric case is ##\Phi = EA## with E the electric field strength in Newton/Coulomb and A the area in m2 . In other words, I get $$\Phi = \oint {\overline {D}\over \varepsilon_0}\; \overline{dS} = {Q_{enc}\over \varepsilon_0}$$ and the units are Nm2/C.
We are still in part (a) first question. I agree that ##Q_{enc} = \rho_s \, 4\pi \,r^2## with ##r = 1 m##.
second and third (a) questions remain unanswered ?
---
Moving on to part (b) first question:
Your exercise composer makes life difficult by re-using symbol ##r## in r = 1.5 m where ##D## is asked for. We no longer need the ##\varepsilon_0##.
You are smart enough to replace ##r## by ##R## (without explaining
##\ ##
Flux is a measure of the flow of a physical quantity through a given surface or region. In the context of electromagnetism, it refers to the flow of electric field lines through a surface.
To calculate the flux through a certain radius, you will need to use the equation Φ = E x A x cos(θ), where Φ is the flux, E is the electric field strength, A is the area of the surface, and θ is the angle between the electric field lines and the surface. You will also need to take into account the direction of the electric field and the orientation of the surface.
Concentric charged spheres are two or more spherical objects with different charges that share the same center point. The electric field between the spheres is dependent on the charges and radii of the spheres.
The radius of the spheres affects the flux through them because it determines the surface area through which the electric field lines pass. As the radius increases, the surface area and the flux also increase.
Calculating flux through concentric charged spheres is important in understanding and predicting the behavior of electric fields in various systems, such as electronic circuits, capacitors, and particle accelerators. It also has practical applications in industries such as telecommunications, where the flux through a certain radius can affect the strength and quality of signals. Additionally, it is crucial in studying the behavior of charged particles in space, such as the Earth's magnetic field and the solar wind.