Calculating the flux through the spherical surfaces at certain radius

[falyusuf]

Homework Statement

Point charges 5 uC, -3 uC, 2 uC and 10 uC are located at (-12, 0,5). (0, 3,-4),(2, -6, 3) and (3, 0, 0), respectively. Calculate the flux through the spherical surfaces at:
i) r= 1
ii) r= 10
iii) r=15

* u = 10^-6 *

Relevant Equations

Attached below.

Relevant Equation:

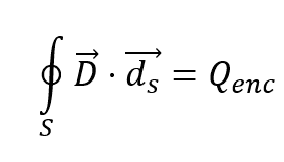
My attempt:

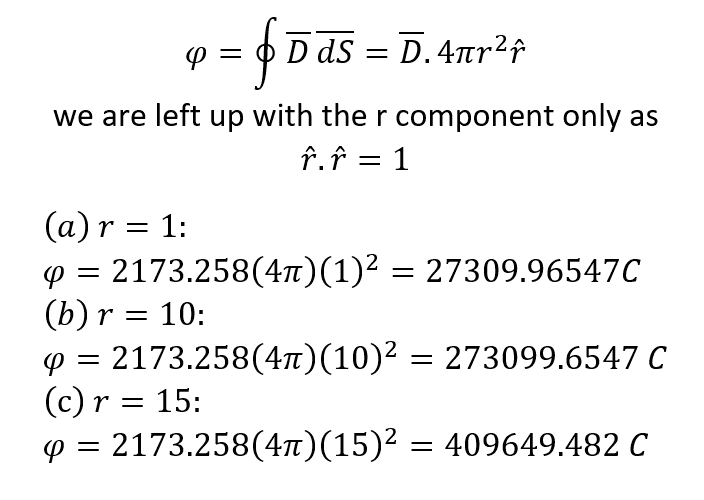
Could someone please confirm my answer?

 

[BvU]

You can't magically greate 10 digit accuracy results from 1 digit givens !

What is $Q_{enc}$ for $r= 1$ ?

$\$

 

[falyusuf]

You can't magically greate 10 digit accuracy results from 1 digit givens !

What is $Q_{enc}$ for $r= 1$ ?

$\$

Yes the answers I got were not reasonable and tried to figure out my mistakes but I couldn't.

I think it's -3 uC as r in the point (0, 3,-4) is 0, which is less than r=1.
so, the total charge enclosed is -3 uC.

 

[BvU]

I must asssume you have correctly given the problem statement

Calculate the flux through the spherical surfaces at:
i) r= 1

etc. And my interpretation is that such spheres are centered at the origin. So that the enclosed charge is zero for $r=1$.
And that you are making a fairly simple exercise quite complicated unnecessarily.

Like in the other problem: what are the units for flux in your textbook ?

$\$

 

[falyusuf]

Like in the other problem: what are the units for flux in your textbook ?

It's Coulomb.

 

[falyusuf]

And my interpretation is that such spheres are centered at the origin. So that the enclosed charge is zero for r=1.

Sorry, I didn't get it. Could you explain further?

 

[BvU]

It's Coulomb.

View attachment 292834

Confusing (for me, at least). SI unit for electric flux is different.

Sorry, I didn't get it. Could you explain further?

The exercise asks for the flux through a spherical shell with radius 1 around the origin (then 10, then 15).

I don't understand what you do with your $\overline{R_1}$ etc.

* u = 10^-6 *

There is a $\mu$ under the 'insert symbol' button:

But (much better): with a little $\LaTeX$ you can do all kinds of math. ##\mu## becomes $\mu$

There is a guide button at lower left:

$\$

 

[falyusuf]

I don't understand what you do with your R1― etc.

I assume that R1 is the vector between point 1 and the origin and found it by

 

[BvU]

What would you need that vector for ?

$\$

 

[falyusuf]

What would you need that vector for ?

$\$

Get its length and substitute it in this formula:

 

[BvU]

Seems to me $\overline {a_R}$ is a unit vector. Right ?

This formula calculates $\overline D$ at the origin. Not what you want. The exercise asks for a flux (in your case apparently an electric displacement flux).

$\$

 

[falyusuf]

Seems to me aR― is a unit vector. Right ?

Seems to me aR― is a unit vector. Right ?

Yes. I think about it more and find that it'll be easier to get r from the given points using this formula:

and then simply;

Right?

 

[BvU]

Makes much more sense to me than post #1 !
And no hassle with 10-digit numbers either

$\$

 

[falyusuf]

Makes much more sense to me than post #1 !
And no hassle with 10-digit numbers either

$\$

Thank you so much. Appreciate your help